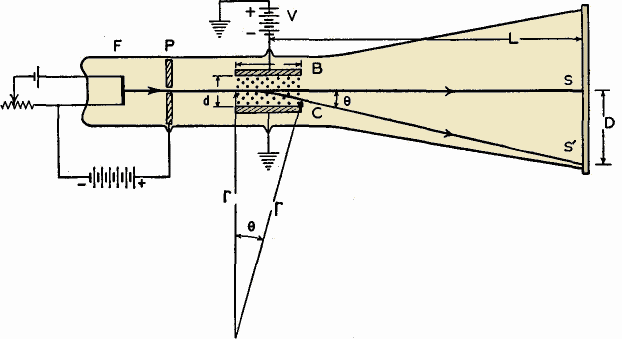
The Mass of the Electron

Author: J.B. Hoag

Consider a glass tube, highly evacuated, cylindrical in shape, with a filament sealed in at one end. In front of the filament let there be a metal plate with a hole in the center and a wire leading to the outside of the tube. On the other end of the tube, on the inside wall, let there be a thin layer of a white powder called phosphorescent zinc sulfide. Now let us heat the filament by sending an electric current through it, and let us fasten a battery between the filament and the metal plate in such a manner as to make the metal plate positive with respect to the filament. Then, the small bits of electricity, electrons, emitted by the filament will be attracted toward the positively charged plate. Some of these in fact will succeed in passing through the small hole in the plate to travel in a straight line down the tube and strike the coated surface at the other end where they produce a bright green spot.

Fig. 1 B. Measurement of the mass and velocity of the electron. (From E. & N. P.)

Now, as in Fig. 1 B, let us deflect the stream of electrons (it is called a cathode ray) by means of an electrical field placed across its path. This can be accomplished by means of two metal plates B and C, and battery V, as in the figure. It will then be found that the spot of light moves sideways from the central spot S to S'.

Next we shall add a magnetic field at right angles to the electron beam, and also at right angles to the electrical field. If this magnetic field is properly adjusted, it will just compensate for the deflection of the beam caused by the electrical field. The green spot on the screen will return to its original position S. By measuring the strength of the electric and magnetic fields when this condition has been attained, it is possible to compute the ratio of the charge to the mass of one of the electrons in the beam. Because we already know the charge, it is a simple matter to compute the mass of the electron. This was first done in a crude way by J. J. Thomson in 1897.

There are many other indirect methods of measuring the mass of an electron. The value is 9.11·10^-28 gram. This extremely small mass has never been measured by any direct method. It is so small that five hundred billion billion billion electrons would be needed to make up 1 pound. The mass of the electron is essentially constant unless the electron is traveling very fast. The faster the electron travels, the greater its mass, in agreement with experimental measurements and with theoretical equations obtained from the Relativity Theory.