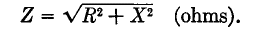Reactance and Impedance

Author: J.B. Hoag

The opposition which a resistor offers to the flow of either direct or alternating current is called resistance.

The opposition which a pure inductance (an inductor without resistance or capacitance) offers to the flow of an alternating current is called its inductive reactance and is represented by X_L. It will be greater, the greater the inductance L (henries) and the higher the frequency f (cycles per second), and in direct proportion in both cases. Thus

X_L = 2πfL   (ohms).

The opposition to the flow of alternating current which is set up by a pure condenser (capacitor without resistance or inductance) is called capacitative reactance and is represented by X_L. The greater the capacitance C (farads) and/or the greater the frequency f (cycles per second), the less X_c will be. Thus

The opposing effect of a capacitance and an inductance connected together one after the other (in series) is called the total reactance, X, of the circuit. It is given by:

X = X_L - X_c    (ohms).

The inductive reactance is taken as positive.

The total opposition to alternating current flow, set up by a pure resistance, inductance, and capacitance in series with each other, is called the impedance of the circuit and is given by

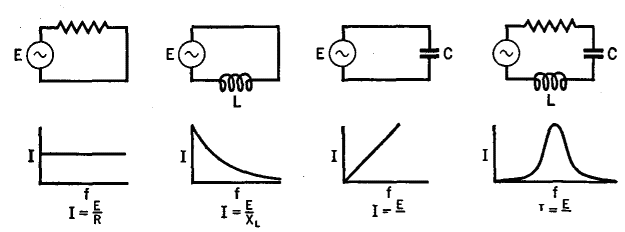
It is to be noted that R and X are not added algebraically but as though they were at right angles to each other.

Ohm's law for an a.c. circuit is:

E = IZ,

as contrasted with E = IR for a d.c. circuit.

The currents I (r.m.s. values) which flow under the conditions discussed above are shown graphically in Fig. 5 A, where the frequency of the oscillator is raised from zero (d.c.) to higher and higher values.

Fig. 5 A. Current from an a.c. generator of variable frequency

Comparative reactances are given in Table 5 A and should be examined carefully by the student.

TABLE 5A. NUMERICAL EXAMPLES OF REACTANCE
	Frequency Cycles per Second	Reactance Ohms
L = 0.1 h.	60 60,000	XL = 38 38,000
L = 1h.	60 60,000	XL = 380 380,000
L = 100 h.	60 60,000	XL = 38,000 38,000,000
C = 0.01 μfd.	60 60,000	Xc = 300,000 300
C = 0.1 μfd.	60 60,000	30,000 30
C = 1 μfd.	60 60,000	3,000 3
C = 10 μfd.	60 60,000	300 0,3