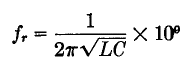Series Resonance

Author: J.B. Hoag

When two bodies, or two currents, or two voltages, oscillate at the same frequency they are said to be in resonance. A series LCR circuit can be built which resonates to a generator of given frequency. Then the current which flows through the circuit will have its greatest effective value. This is accomplished by choosing the inductive and capacitive reactances equal to each other. From the equations for the reactances, it is easily proven that the resonant frequency is given by

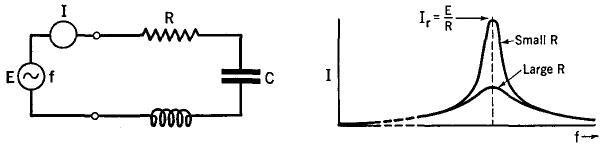
where f_r is in cycles per second, 2π = 6.28,10⁶ = 1 million, L is the inductance in microhenries (μH), and C is the capacitance in picofarads (pF). This is one of the most important equations in radio. Note that the resistance of the circuit does not appear in the equation. At resonance, the only opposition to the flow of the current is that due to the resistance, i.e., I_r = E/R and not I = E/Z.

Fig. 6 A. A series circuit and its resonance curve

The current in the " tuned " or resonant series circuit is indicated at the peak of the " resonance " curve of Fig. 6 A. Note that if the total resistance of the circuit is large, the curve is broader and flatter, and vice versa.