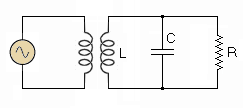
The L to C Ratio

Author: J.B. Hoag

In order that a circuit shall resonate to a given frequency f_r, the product LC must have a definite value given by LC = 1/(2πf_r)². This does not tell us, however, whether the product shall be made up of a large L and a small C or vice versa. Within limits, an increase in the number of turns of wire in a coil increases its reactance faster than its resistance. Hence, for circuits alone, or for those connected to high load resistances, such as a vacuum tube, the coils should be made with a relatively large inductance, i.e., the L/C ratio should be large.

Fig. 6 C. If R is small, the LC circuit will be heavily loaded and will have a low Q. Making the ratio L/C small helps to keep Q large.

When the load on a resonant circuit (R in Fig. 6 C) is small, say only a few thousand ohms, as in transmitters and induction heaters, a majority of the energy loss takes place in the load. The coil's resistance plays only a negligible role. In this case, it can be shown that L should be comparatively small and C large if Q is to be satisfactorily high.