| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Slope and Velocity; the Hyperreal Line Slope and Velocity; the Hyperreal Line  Slope and Velocity; The Hyperreal Line - Part 8 Slope and Velocity; The Hyperreal Line - Part 8 |
|






|
|
Slopes Along Curves
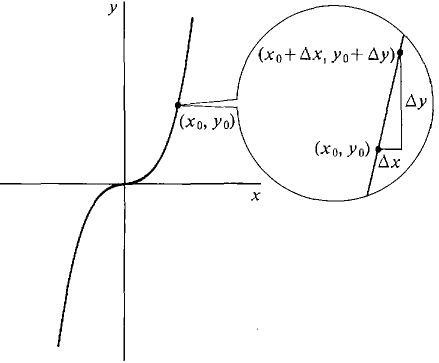
The same method can be applied to other curves. The third degree curve y = x3 is shown in Figure 1.4.6. Let (x0, y0) be any point on the curve y = x3, and let Δx be a positive or a negative infinitesimal. Let Δy be the corresponding change in y along the curve.
Figure 1.4.6 In Figure 1.4.7, Δx and Δy are shown under a microscope. We again define the slope at (x0, y0) by [slope at (x0, y0)] = [the real number infinitely close to
Figure 1.4.7 We now compute the hyperreal number
and finally
In the next section we shall develop some rules about infinitesimals which will enable us to show that since Δx is infinitesimal, 3x0 Δx + (Δx)2 is infinitesimal as well. Therefore the hyperreal number 3x02 + 3x0 Δx + (Δx)2 is infinitely close to the real number 3x02, whence [slope at (x0,y0)] = 3x02. For example, at (0, 0) the slope is zero, at (1, 1) the slope is 3, and at (2, 8) the slope is 12. We shall return to the study of the slope of a curve in Chapter 2 after we have learned more about hyperreal numbers. From the last example it is evident that we need to know how to show that two numbers are infinitely close to each other. This is our next topic.
|
|
Home  Real and Hyperreal Numbers Real and Hyperreal Numbers  Slope and Velocity; the Hyperreal Line Slope and Velocity; the Hyperreal Line  Slope and Velocity; The Hyperreal Line - Part 8 Slope and Velocity; The Hyperreal Line - Part 8 |
|
Last Update: 2010-11-25



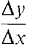 ]
]
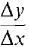 .
.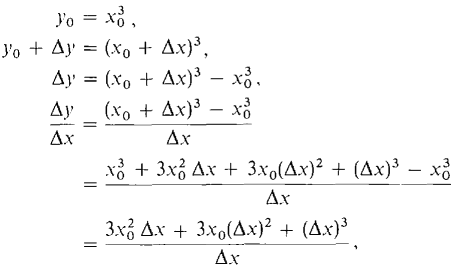
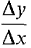 = 3x02 + 3x0 Δx + (Δx)2.
= 3x02 + 3x0 Δx + (Δx)2.