Example 1

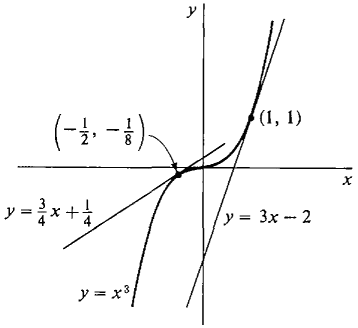
For the curve

y = x³,

find the tangent lines at the points (0,0), (1,1), and (-½, -⅛) (Figure 2.2.2).

The slope is given by

f'(x) = 3x².

At x = 0,

f'(0) = 3 · 0² = 0.

The tangent line has the equation

y = 0(x - 0) + 0, or y = 0.

At x = 1,

f'(1) = 3,

whence the tangent line is

y = 3(x - 1) + 1, or y = 3x - 2.

At x = -½,

f'(-½) = 3 -(-½)² = ¾,

so the tangent line is

y = ¾(x - (-½)) + (-⅛), or y = ¾x + ¼