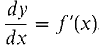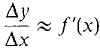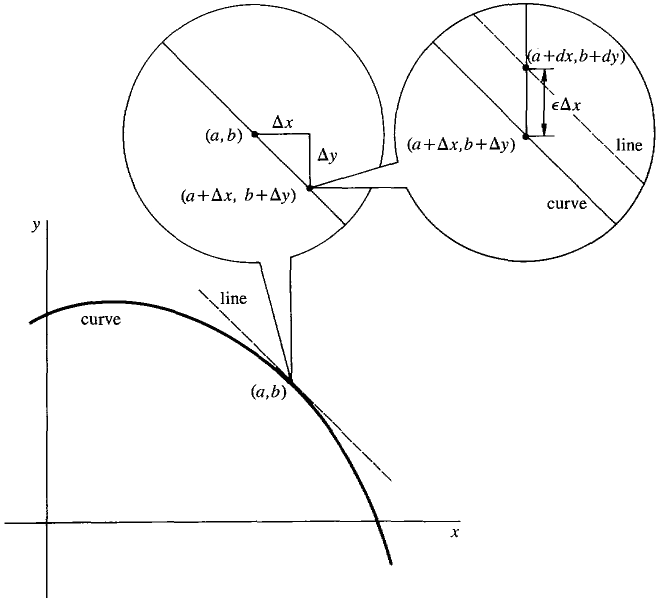Definition of Differentials

Compare this equation with

The quotient dy/dx is a very convenient alternative symbol for the derivative f'(x). In fact we shall write the derivative in the form dy/dx most of the time.

The differential dy depends on two independent variables x and dx. In functional notation,

dy = df(x, dx)

where df is the real function of two variables defined by

df(x,dx) = f'(x)dx.

When dx is substituted for Δx and dy for f'(x) dx, the Increment Theorem takes the short form

Δy = dy + ε dx.

	If want to experiment with tangents to curves and see the relation to the differential, you should download the Tangent simulation from the Learning by Simulations site.

The Increment Theorem can be explained graphically using an infinitesimal microscope. Under an infinitesimal microscope, a line of length Δx is magnified to a line of unit length, but a line of length ε Δx is only magnified to an infinitesimal length ε. Thus the Increment Theorem shows that when f'(x) exists:

(1)    The differential dy and the increment Δy = dy + ε dx are so close to each other that they cannot be distinguished under an infinitesimal microscope.

(2)    The curve y = f(x) and the tangent line at (x, y) are so close to each other that they cannot be distinguished under an infinitesimal microscope; both look like a straight line of slope f'(x).

Figure 2.2.3 is not really accurate. The curvature had to be exaggerated in order to distinguish the curve and tangent line under the microscope. To give an accurate picture, we need a more complicated figure like Figure 2.2.4, which has a second infinitesimal microscope trained on the point (a + Δx, b + Δy) in the field of view of the original microscope. This second microscope magnifies ε dx to a unit length and magnifies Δx to an infinite length.