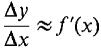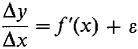| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Differentiation Differentials and Tangent Lines Increment Theorem and Proof |
|
 Search the VIAS Library | Index
|
  |
Increment Theorem and Proof
INCREMENT THEOREM Let y = f (x). Suppose f'(x) exists at a certain point x, and Δx is infinitesimal. Then Δy is infinitesimal, and Δy = f'(x) Δx + ε Δx for some infinitesimal ε, which depends on x and Δx. PROOF Case 1 Δx = 0. In this case, Δy = f'(x) Δx = 0, and we put ε = 0. Case 2 Δx ≠ 0. Then
so for some infinitesimal ε,
Multiplying both sides by Δx, Δy = f '(x) Δx + ε Δx.
|
|
| Home Differentiation Differentials and Tangent Lines Increment Theorem and Proof |
|
Last Update: 2010-11-25