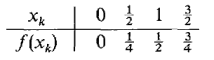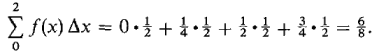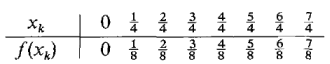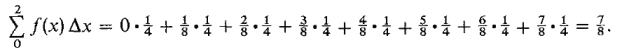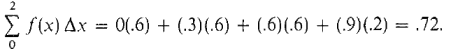Riemann Sum and Area of a Triangle

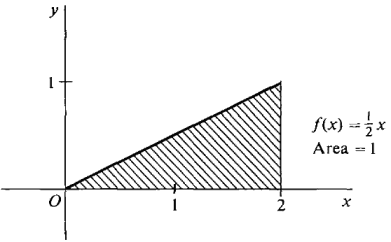
Let f(x) = ½x. In Figure 4.1.6, the region under the curve from x = 0 to x = 2 is a triangle with base 2 and height 1, so its area should be

A = ½bh = 1.

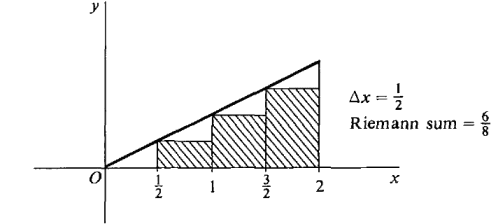
Figure 4.1.6

Let us compare this value for the area with some Riemann sums. In Figure 4.1.7, we take Δx = ½. The interval [0,2] divides into four subintervals [0, ½], [½, 1], [1, 3/2], and [3/2, 2]. We make a table of values of f(x) at the lower endpoints.

Figure 4.1.7

The Riemann sum is then

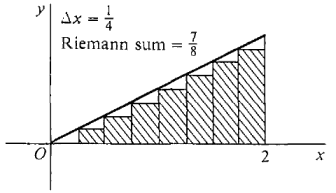
In Figure 4.1.8, we take Δx = ¼. The table of values is as follows.

Figure 4.1.8

The Riemann sum is

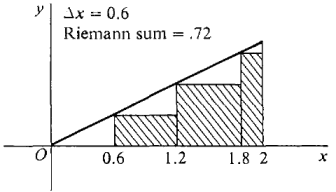
We see that the value is getting closer to one.

Finally, let us take a value of Δx that does not divide evenly into the interval length 2. Let Δx = 0.6. We see in Figure 4.1.9 that the interval then divides into three subintervals of length 0.6 and one of length 0.2, namely [0, 0.6], [0.6, 1.2], [1.2, 1.8], [1.8, 2.0].

Figure 4.1.9

The Riemann sum is