| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  The Definite Integral The Definite Integral  Definite Integral Definite Integral |
|||||






|
|||||
Definite Integral
We are now ready to define the central concept of this chapter, the definite integral. Recall that the derivative was defined as the standard part of the quotient Δy/Δx and was written dy/dx. The "definite integral" will be defined as the standard part of the infinite Riemann sum
and is written notation. The Σ is changed to the long thin S, i.e., DEFINITION Let f be a continuous function on an interval I and let a < b be two points in I. Let dx be a positive infinitesimal. Then the definite integral of f from a to b with respect to dx is defined to be the standard part of the infinite Riemann sum with respect to dx, in symbols
We also define
By this definition, for each positive infinitesimal dx the definite integral
is a real function of two variables defined for all pairs (u, w) of elements of I. The symbol x is a dummy variable since the value of
does not depend on x. In the notation integral, we always use matching symbols for the infinitesimal dx and the dummy variable x. Thus when there are two or more variables we can tell which one is the dummy variable in an integral. For example, x2t can be integrated from 0 to 1 with respect to either x or t. With respect to x,
(where dx = 1/H), and we shall see later that
With respect to t, however,
and we shall see later that
The next two examples evaluate the simplest definite integrals. These examples do it the hard way. A much better method will be developed in Section 4.2.
|
|||||
Home  Integral Integral  The Definite Integral The Definite Integral  Definite Integral Definite Integral |
|||||
Last Update: 2010-11-26



 . Thus the Δx is changed to dx in analogy with our differential
. Thus the Δx is changed to dx in analogy with our differential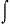 , to remind us that the integral is obtained from an infinite sum. We now state the definition carefully.
, to remind us that the integral is obtained from an infinite sum. We now state the definition carefully.


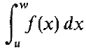

 for the Riemann sum and
for the Riemann sum and  for the
for the