| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  Theorems of Calculus Theorems of Calculus  Theorem 3: The Addition Property Theorem 3: The Addition Property |
|






|
|
Theorem 3: The Addition Property
THEOREM 3 (The Addition Property) Suppose f is continuous on an interval I. Then for all a, b, c in I,
This property is illustrated in Figure 4.2.5 for the case a < b < c. The Addition Property holds even if the points a, b, c are in some other order on the real line, such as c < a < b.
Figure 4.2.5 PROOF First suppose that a < b < c. Choose a dx that evenly divides the first interval length b-a. This simplifies our computation because it makes b a partition point, b = a + H dx. Then, as Figure 4.2.6 suggests,
Taking standard parts we have the desired formula
Figure 4.2.6 To illustrate the other cases, we prove the Addition Property when c < a < b. The previous case gives
Since reversing the endpoints changes the sign of the integral,
and the desired formula
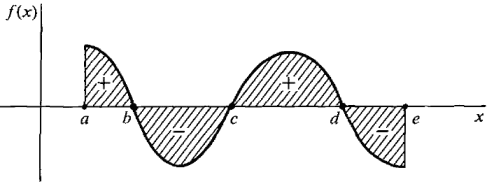
follows. The definite integral of a curve can be thought of as area even if the curve crosses the x-axis. The curve in Figure 4.2.7 is positive from a to b and negative from b to c, crossing the x-axis at b. The integral integral
is equal to the area from a to b minus the area from b to c. The definite integral The definite integral and does not depend on the dummy variable t. If we replace u by a constant a and v by the variable x, we obtain a real function of one variable x, given by
Our fourth theorem states that this new function is continuous.
Figure 4.2.7
|
|
Home  Integral Integral  Theorems of Calculus Theorems of Calculus  Theorem 3: The Addition Property Theorem 3: The Addition Property |
|
Last Update: 2006-11-05




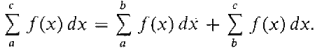





 is a positive number and the
is a positive number and the is a negative number. By the Addition Property, the integral
is a negative number. By the Addition Property, the integral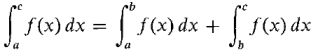
 always gives the net area between the x-axis and the curve, counting areas above the x-axis as positive and areas below the x-axis as negative.
always gives the net area between the x-axis and the curve, counting areas above the x-axis as positive and areas below the x-axis as negative.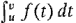 is a real function of two variables u and v
is a real function of two variables u and v