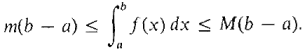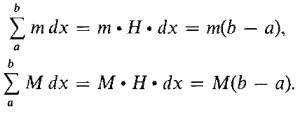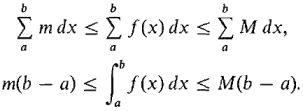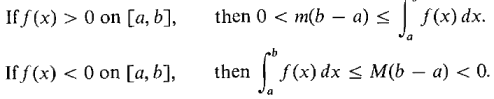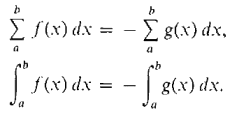Theorem 2: The Rectangle Property

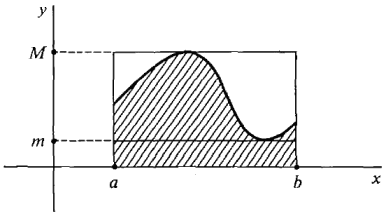
The Extreme Value Theorem is needed to show that the minimum value m and maximum value M exist. The rectangle of height m is called the inscribed rectangle of the region, and the rectangle of height M is called the circumscribed rectangle. From Figure 4.2.3, we see that the inscribed rectangle is a subset of the region under the curve, which is in turn a subset of the circumscribed rectangle. The Rectangle Property says that the area of the region is between the areas of the inscribed and circumscribed rectangles.

Figure 4.2.3: The Rectangle Property

PROOF

By Theorem 1, any positive infinitesimal may be chosen for dx. Let us choose a positive infinite hyperinteger H and let dx = (b-a)/H. Then dx evenly divides b-a; that is, the interval [a, b] is divided into H subintervals of exactly the same length dx. Then

For each x, we have m ≤ f (x) ≤ M. Adding up and taking standard parts, we obtain the required formula.

One useful consequence of the Rectangle Property is that the integral of a positive function is positive and the integral of a negative function is negative:

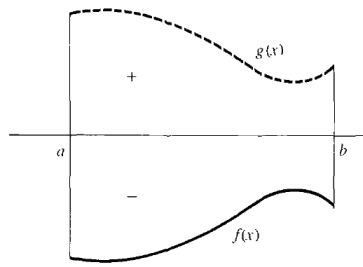
The definite integral of a negative function f(x) = -g(x) from a to b is just the negative of the area of the region above the curve and below the x axis. This is because

f(x)dx = -g(x)dx,

(See Figure 4.2.4.)

Figure 4.2.4