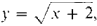The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Integral Theorems of Calculus Problems
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Problems

In Problems 1-14, find an antiderivative of the given function.

04_integration-163.gif 04_integration-164.gif
04_integration-165.gif

Evaluate the definite integrals in Problems 18-22.

04_integration-166.gif 04_integration-167.gif

In Problems 23-27 an object moves along the y-axis. Given the velocity v, find how far the object moves between the given times t0 and t1.

04_integration-168.gif
25 v = 3,  f0 = 2, t1 = 6
26 v = 3r2, f0 = 1, t1 = 3
27 v = 10r-2, f0 = 1, t1 = 100

In Problems 28-32, find the area of the region under the curve y = /(x) from a to b.

28 y = 4- x2,  a = -2, b = 2
29 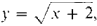04_integration-169.gif a = -2, b = 2
30 y = 9x - x2, a = 0, b = 3
31 y = √v - x, a = 0, b = 1
32 y = 3x1 3, a = 1, b = 8

 

33 If F'(t) = t - 1 for all t and F(0) = 2, find F(2).
34 If F'(x) = 1 - x2 for all x and F(3) = 5, find F(- 1).
35 Suppose F(x) and G(x) have continuous derivatives and F'(x) + G'(x) = 0 for all x. Prove that F(x) + G(x) is constant.
36

Suppose F(x) and G(x) have continuous derivatives such that F'(x) < G'(x) for all x. Prove that F(b) - F(a) ≤ G(b) - G(a)

where a < b.
37 Prove that a function F(x) has a constant derivative if and only if F(x) is linear, i.e., of the form F(x) = ax + b.
38 Prove that a function F(x) has a constant second derivative if and only if F(x) has the form F(x) = ax2+ bx + c.
39 Suppose that F"(x) = G"(x) for all x. Prove that F(x) and G(x) differ by a linear function, that is, G(x) = F(x) + ax + b for some real numbers fl and b.

Home Integral Theorems of Calculus Problems

Last Update: 2006-11-25