Proof of the Fundamental Theorem

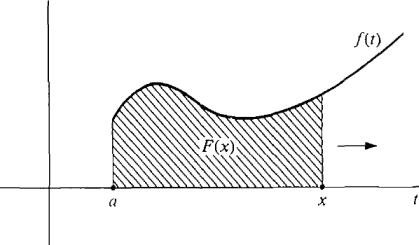
We conclude this section with a proof of the Fundamental Theorem of Calculus.

PROOF

(i) Let f(x) be the area under the curve y = f(t) from a to x,

Imagine that the vertical line cutting the t-axis at x moves to the right as in Figure 4.2.11.

Figure 4.2.11

We show that the rate of change of F(x) is equal to the length f (x) of the moving vertical line.

Suppose x increases by an infinitesimal amount ∆x > 0. Then

is the area of an infinitely thin strip of width ∆x and height infinitely close to f(x). By the Rectangle Property the area of the strip is between the inscribed and circumscribed rectangles (Figure 4.2.12),

m ∆x ≤ F(x + ∆x) - F(x) ≤ M ∆x.

Figure 4.2.12

Dividing by ∆x,

Since f is continuous at x, the values m and M are both infinitely close to f(x), and therefore

The proof is similar when ∆x < 0. Hence F'(x) = f (x).

PROOF

(ii) Let F(x) be any antiderivative of f Then, by (i),

In Section 3.7 on curve sketching, we saw that every function with derivative zero is constant. Thus

for some constant C₀. Then

so