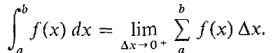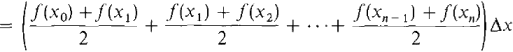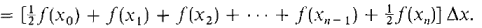| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  Numerical Integration Numerical Integration  Introduction Introduction |
|






|
|
Numerical Integration
In numerical integration, one computes an approximate value for the definite integral rather than finding an exact value. In this section we shall present two methods of numerical integration, called the Trapezoidal Rule and Simpson's Rule. The Fundamental Theorem of Calculus gives us a method of computing the definite integral of a given continuous function f from a to b. The method is to find, by trial and error, an antiderivative F off and then to use the equation
When the method works, it provides an exact value for the integral. However, the method succeeds only if the antiderivative happens to be a function that can be described in a simple way. For many integrals one cannot find a formula for the antiderivative, and the method fails. Such integrals can still be computed approximately using numerical integration. The Trapezoidal Rule and Simpson's Rule can always be applied and do not use the antiderivative. They are easy to carry out on a computer or hand calculator. We already discussed one method of approximating the definite integral in Section 4.1, the Riemann sum. The Trapezoidal Rule is a modified form of the Riemann sum, which gives a much closer approximation for a given amount of effort. Simpson's Rule is a further modification that gives still better approximations. Let f be a continuous function on an interval I, and let a < b in I. By definition, for each positive infinitesimal dx the definite integral
is the standard part of the infinite Riemann sum
In Section 4.1, examples were worked out to show that the finite Riemann sums become very close to the definite integral when Δx is small; that is, the finite Riemann sums approximate the definite integral. In Section 4.2, we saw that the definite integral is the limit of the finite Riemann sums as Δx → 0+:
The Riemann sum, which is a sum of areas of rectangles, is a rather inefficient approximation of the definite integral. We can usually get a much closer approximation with the same amount of work by adding up areas of trapezoids instead of rectangles, forming the Trapezoidal Rule suggested by Figure 4.6.1. The Trapezoidal Rule also provides a formula, called an error estimate, which tells us how close the approximation is to the exact value of the definite integral.
Figure 4.6.1 Choose a positive integer n and divide the interval [a, b] into n subintervals of equal length Δx = (b - a)/n. The partition points are a = x0, x1, x2,..., xn, = b. The trapezoidal approximation is the area of the region under the broken line connecting the points (x0, f(x0)), (x1, f(xl)), ..., (xn , f(xn)). Since all of these points lie on the curve y = f(x), the broken line closely follows the curve. So one would expect the area of the region under the broken line to closely approximate the area under the curve. Consider a single subinterval [xm, xm+1] of width Δx. The region under the line segment connecting the two points (xm, f(xm)), (xm+1, f(xm+1)) is a trapezoid and its area is
The sum of the areas of the trapezoids is a modified Riemann sum
|
|
Home  Integral Integral  Numerical Integration Numerical Integration  Introduction Introduction |
|
Last Update: 2010-11-26


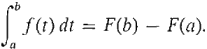
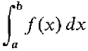
 ,
,