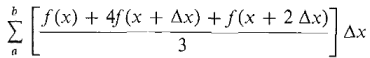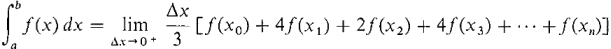Elementary Calculus: Simpson's Rule

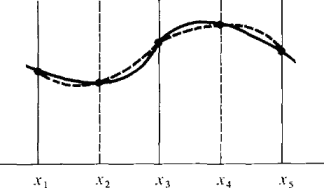
We now turn to Simpson's Rule, for which the number of subintervals n must be even. As before, we divide the interval [a, b] into n subintervals of equal length Δx with the n + 1 partition points

We shall use subintervals of length 2 Δx rather than Δx. On each of the n/2 subintervals

of length 2 Δx we approximate the curve y = f(x) by a parabolic arc that meets the curve at both endpoints and the midpoint of the subinterval, as shown in Figure 4.6.3. We then add up the areas under each of the parabolic arcs to obtain an approximation to the area under the curve, which is the definite integral. We begin with a lemma that gives a formula for the area of the region under one parabolic arc.

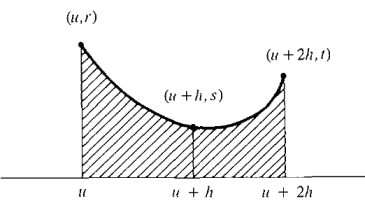
LEMMA

The area of the region under the parabola through three points

(u, r), (u + h, s), and (u + 2h, t)

(shown in Figure 4.6.4) is

h/3 (r + 4s + t)

The lemma is proved at the end of this section. Using the lemma, we find that the area of the region under one parabolic arc from x_k to x_k ₊ ₂ is

It follows that the sum of the n/2 regions under the parabolic arcs is a modified Riemann sum,

= Δx/3 [f(x₀) + 4f(x₁) +2f(x₂) +4f(x₃) +2f(x₄)+ ... +4f(x_n-1) +f(x_n)].

This modified Riemann sum is Simpson's approximation to the definite integral. Note the sequence of coefficients,

Like the trapezoidal approximation, it is easily computed on a computer or hand calculator.

THEOREM 2

For a continuous function f on [a, b], Simpson's approximation approaches the definite integral as Δx → 0 ⁺ ,

Simpson's approximation is almost as easy to calculate as the trapezoidal approximation, but is much more accurate. Simpson's Rule is an error estimate that involves the fourth derivative of the function and the fourth power of Δx.

SIMPSON'S RULE

Suppose the function f has a fourth derivative on the interval [a, b] that has absolute value at most M,

|f⁽⁴⁾(x)| ≤ M for a ≤ x ≤ b.

If [a, b] is divided into an even number of subintervals of length Δx, then Simpson's approximation to the definite integral has the error estimate

PROOF OF THE LEMMA

The algebra is simpler if the y-axis is drawn through the second point, so that u + h = 0, and the three points have coordinates

(-h, r), (0, s), (h, t).

Suppose the parabola has the equation y = ax² + bx + c. Then the area under the parabola is

When we substitute the coordinates of the three points (- h, r), (0, s), (h, t) into the equation for the parabola, we obtain the three equations

r = ah² - bh + c,

s = c,

t = ah² + bh + c.

Add the first and third equations and solve for a:

Finally, substitute the above expression for a and s for c in the equation for the area: