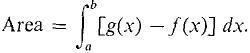Area Between Two Curves

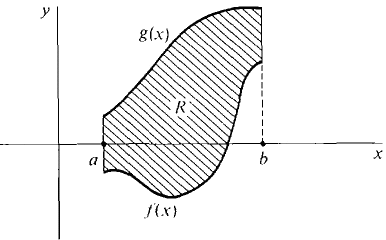
We shall use the Infinite Sum Theorem several times in this chapter. As a first illustration of the method, we derive again the formula from Chapter 4 for the area of the region between two curves, shown in Figure 6.1.3.

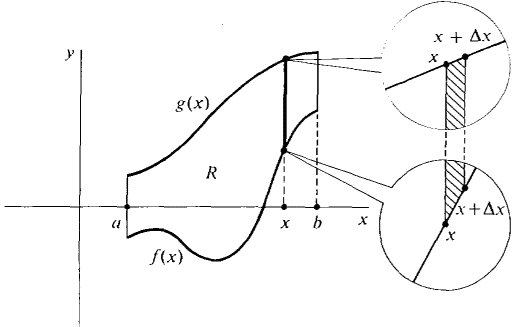
Figure 6.1.3

AREA BETWEEN TWO CURVES

where f and g are continuous and

f(x) ≤ g(x) for a ≤ x ≤ b.

The justification of a definition resembles the proof of a theorem, but it shows that an intuitive concept is equivalent to a mathematical one. We shall now use the Infinitive Sum Theorem to give a justification of the formula for the area between two curves.

JUSTIFICATION
We write A(a, b) for the intuitive area of the region R between f(x) and g(x) from a to b. A(u, w) has the Addition Property. Slice R into vertical strips of infinitesimal width Δx. Each strip is almost a rectangle of height g(x) - f(x) and width Δx (Figure 6.1.4). The area ΔA = A(x, x + Δx) of the strip is infinitely close to the area of the rectangle compared to Δx,

ΔA x [g(x) - f(x)] Δx       (compared to Δx).

The infinite sum theorem now shows that A(a, b) is the integral of g(x) - f(x) from a to b.

Figure 6.1.4