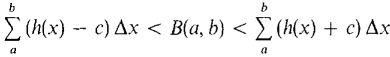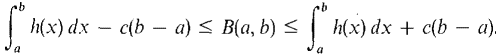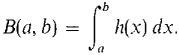Infinite Sum Theorem - Proof

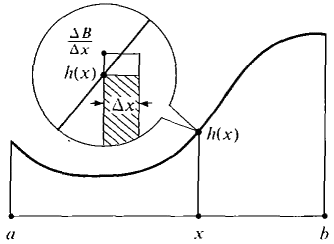
For example,

3 Δx + 5 Δx² ≈ 3 Δx - Δx² + Δx³       (compared to Δx)

but 

3 Δx + 5 Δx² ≈ 2 Δx (compared to Δx).

The Infinite Sum Theorem is used when we have a quantity B(u, w) depending on two variables u < w in [a, b], and the total value B(a, b) is the sum of infinitesimal pieces

ΔB = B(x, x + Δx).

he theorem gives a method of expressing B(a, b) as a definite integral.

Let B(u, w) be a real function of two variables that has the Addition Property in the interval [a, b] — i.e.,

B(u, w) = B(u, v) + B(v, w) for u < v < w in [a, b].

Suppose h(x) is a real function continuous on [a, b] and for any infinitesimal subinterval [x, x + Δx] of [a, b],

ΔB ≈ h(x) Δx (compared to Δx).

Then B(a, ft) is equal to the integral

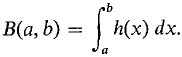
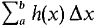Intuitively, the theorem says that if each infinitely small piece AB is infinitely close to h(x) Δx compared to Δx, then the sum B(a, b) of all these pieces is infinitely close to (Figure 6.1.2). This is why we call it the Infinite Sum Theorem.

Figure 6.1.2