| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Length of a Curve Length of a Curve  Theorem and Proof Theorem and Proof |
|






|
|
Theorem and Proof
We next prove a theorem which shows the connection between the length of an arc and the area of a sector of a circle. Given two points P and Q on a circle with center 0, the arc PQ is the portion of the circle traced out by a point moving from P to Q in a counterclockwise direction. The sector POQ is the region bounded by the arc PQ and the radii OP and OQ as shown in Figure 6.3.7.
Figure 6.3.7 THEOREM Let P and Q be two points on a circle with center 0. The area A of the sector POQ is equal to one half the radius r times the length s of the arc PQ, A = ½rs. DISCUSSION The theorem is intuitively plausible because if we consider an infinitely small arc As of the circle as in Figure 6.3.8, then the corresponding sector is almost a triangle of height r and base As, so it has area ΔA ≈ ½r Δs (compared to Δs). Summing up, we expect that A = ½rs.
Figure 6.3.8 We can derive the formula C = 2πr for the circumference of a circle using the theorem. By definition, π is the area of a circle of radius one,
Then a circle of radius r has area
Therefore the circumference C is given by A = ½rC, πr2 = ½rC, C = 2πr.
Figure 6.3.9 PROOF OF THEOREM To simplify notation assume that the center 0 is at the origin, P is the point (0, r) on the x-axis, and Q is a point (x, y) which varies along the circle (Figure 6.3.9). We may take y as the independent variable and
use the equation depend on y. Our plan is to show that
First, we find dx/dy:
Using the definition of arc length,
The triangle OQR in the figure has area ½xy, so the sector has area
Then
Thus So A and ½rs differ and only by a constant. But when y = 0, A = ½rs = 0. Therefore A = ½rs. To prove the formula A = ½rs for arcs which are not within a single quadrant we simply cut the arc into four pieces each of which is within a single quadrant.
|
|
Home  Applications of the Integral Applications of the Integral  Length of a Curve Length of a Curve  Theorem and Proof Theorem and Proof |
|
Last Update: 2010-11-25







 for the right half of the circle. Then A and s
for the right half of the circle. Then A and s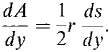



 =
=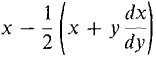 =
=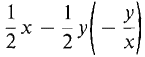 =
= =
=
 ,
,  ,
,