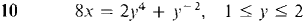Problems

Find the lengths of the following curves.

Hint: Solve for x as a function of y.

17            Find the distance travelled from t = 0 to t = 1 by an object whose motion is x = t^3/2, y = (3 - t)^3/2.

18            Find the distance moved from t = 0 to t = 1 by a particle whose motion is given by

x = 4(1 - t)^3/2, y = 2t^3/2.

19            Find the distance travelled from t = 1 to t = 4 by an object whose motion is given by

x = t^3/2, y = 9t.

20            Find the distance travelled from time t = 0 to t = 3 by a particle whose motion is given by the parametric equations x = 5t², y = t³.

21             Find the distance moved from t = 0 to t = 2π by an object whose motion is x = cos t, y = sin t.

22            Find the distance moved from t = 0 to t = π by an object with motion x = 3 cos 2t, y = 3 sin 2t.

23             Find the distance moved from t = 0 to t = 2π by an object with motion x = cos²t, y = sin² t.

24            Find the distance moved by an object with motion x = e' cos t, y = e' sin t, 0 ≤ r ≤ 1.

25             Let A(t) and L(t) be the area under the curve y = x² from x = 0 to x = t, and the length of the curve from x = 0 to x = t, respectively. Find d(A(t))/d(L(t)).

In Problems 26-30, find definite integrals for the lengths of the curves, but do not evaluate the integrals.

26             y = x³ 0 ≤ x ≤ 1

27            y = 2x² - x + 1, 0 ≤ x ≤ 4

28            x = 1/t, y = t², 1 ≤ t ≤ 5

29             x = 2t + 1, y = √t, 1 ≤ t ≤ 2

30            The circumference of the ellipse x² + 4y² = 1.

31             Set up an integral for the length of the curve y = √x, 1 ≤ x ≤ 2, and find the Trapezoidal Approximation where Δx = ¼.

32            Set up an integral for the length of the curve x = t² - t, y = (4/3)t^3/2, 0 ≤ t ≤ 1, and find the Trapezoidal Approximation where Δt = ¼.

33            Set up an integral for the length of the curve y = 1/x, 1 ≤ x ≤ 5, and find the Trapezoidal Approximation where Δx = 1.

34           Set up an integral for the length of the curve y = x², -1 ≤ x ≤ 1, and find the Trapezoi-

dal Approximation where Δx = ½.

D 35           Suppose the same curve is given in two ways, by a simple equation y = F(x), a ≤ x ≤ b

and by parametric equations x = f(t), y = g(t), c ≤ t ≤ d. Assuming all derivatives are continuous and the parametric curve does not retrace its path, prove that the two formulas for curve length give the same values. Hint: Use integration by change of variables.