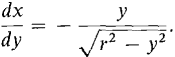| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 4: Example 4: |
|






|
|
Example 4: Surface Of a Sphere
Derive the formula A = 4πr2 for the area of the surface of a sphere of radius r. When the portion of the circle x2 + y2 = r2 in the first quadrant is rotated about the y-axis it will form a hemisphere of radius r (Figure 6.4.12). The surface of the sphere has twice the area of this hemisphere.
Figure 6.4.12 It is simpler to take y as the independent variable, so the curve has the equation x = Then
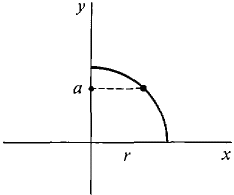
This derivative is undefined at y = 0. To get around this difficulty we let 0 < a < r and divide the surface into the two parts shown in Figure 6.4.13, the surface B generated by the curve from y = 0 to y = a and the surface C generated by the curve from y = a to y = r.
Figure 6.4.13 The area of C is
We could find the area of B by taking x as the independent variable. However, it is simpler to let a be an infinitesimal e. Then B is an infinitely thin ring-shaped surface, so its area is infinitesimal. Therefore the hemisphere has area
½A = B + C ≈ 0 + 2πr(r - ε) ≈ 2πr2 , so ½A = 2πr2, and the sphere has area A = 4πr2.
|
|
Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 4: Example 4: |
|
Last Update: 2006-11-22



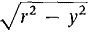 , 0 < y < r.
, 0 < y < r.