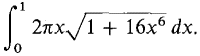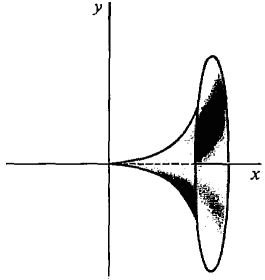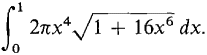| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 5: Rotating a Curve About X-axis and Y-axis Example 5: Rotating a Curve About X-axis and Y-axis |
|






|
|
Example 5: Rotating a Curve About X-axis and Y-axis
Let C be the curve y = x4, 0 < x < 1. (see Figure 6.4.15)
Figure 6.4.15 Set up an integral for the surface area generated by rotating the curve C about (a) the y-axis, (b) the x-axis (see Figure 6.4.16). (a)
Figure 6.4.16 (a) dy/dx = 4x3 A =
We cannot evaluate this integral, so we leave it in the above form. The Trapezoidal Rule can be used to get approximate values. When Δx = 1/10 the Trapezoidal Approximation is A ~ 6.42, error ≤ 0.26. (b)
Figure 6.4.16(b) A =
The Trapezoidal Approximation when Δx = 1/10 is A ~ 3.582 error ≤ 0.9.
|
|
Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Examples Examples  Example 5: Rotating a Curve About X-axis and Y-axis Example 5: Rotating a Curve About X-axis and Y-axis |
|
Last Update: 2010-11-25