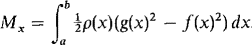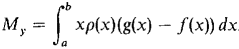| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Some Applications to Physics Some Applications to Physics  Problems Problems |
|






|
|
Problems
In Problems 1-16 below, find (a) the mass, (b) the moments about the x- and y-axes, (c) the center of mass of the given object. 1 A wire on the x-axis, 0 ≤ x ≤ 2 with density ρ(x) = 2. 2 A wire on the x-axis, 0 ≤ x ≤ 4, with density ρ(x) = x3. 3 A wire on the y-axis, 0 ≤ y ≤ 4, whose density is twice the distance from the lower end of the wire times the square of the distance from the upper end. 4 A straight wire from the point (0, 0) to the point (1,1) whose density at each point (x, x) is equal to 3x. 5 A wire of length 6 and constant density k which is bent in the shape of an L covering the intervals [0, 2] on the x-axis and [0, 4] on the y-axis. 6 The plane object bounded by the x-axis and the curve y = 4 - x2, with constant density k. 7 The plane object bounded by the x-axis and the curve y = 4 - x2, with density ρ(x) = x2. 8 The plane object bounded by the lines x = 0,y = x,y = 4 - 3x, with density ρ(x) = 2x. 9 The plane object between the x-axis and the curve y = x2, 0 ≤ x ≤ 1, with density ρ(x) = 1/x. 10 The object bounded by the x-axis and the curve y = x3, 0 ≤ x ≤ 1, with density ρ(x) = 1 - x2. 11 The object bounded by the x-axis and the curve y = 1/x, 1 ≤ x ≤ 2, with density ρ(x) = 12 The disc bounded by x2 + y2 = 4 with density pfx) = 13 The object in the top half of the circle x2 + y2 = 1, with density p(x) = 2|x|. 14 The object between the x-axis and the curve y = 15 The object bounded by the x-axis and the curve y = 4x - x2, with density p(x) = 2x. 16 The object bounded by the curves y = -f(x) and y = f(x), 0 ≤ x ≤ 3, with density ρ(x) = 4/f(x). (f(x) is always positive.) In Problems 17-24, sketch and find the centroid of the region bounded by the given curves.  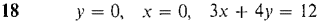 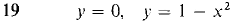 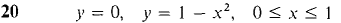 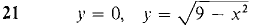   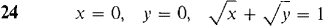
33 Use the formulas in Problem 32 to find the centroid of the region between the curves y = x2 and y = x. 34 A piece of metal weighing 50 lbs is in the shape of a triangle of sides 3, 4, and 5 ft. Find the amount of work required to stand the piece up on (a) the 3 ft side, (b) the 4 ft side. 35 A 4 ft chain lies flat on the ground and has constant density of 5 lbs/ft. How much work is required to lift one end 6 ft above the ground? 36 In Problem 35, how much work is required to lift the center of the chain 6 ft above the ground? 37 A 4 ft chain has a density of 4x lbs/ft at a point x ft from the left end. How much work is needed to lift the left end 6 ft above the ground? 38 In Problem 37, how much work is needed to lift both ends of the chain to the same point 6 ft above the ground? 39 A spring exerts a force of 4x lbs when compressed a distance x. How much work is needed to compress the spring 5 ft from its natural length? 40 A bucket of water weighs 10 lbs and is tied to a rope which has a density of ^ lb/ft. How much work is needed to lift the bucket from the bottom of a 20 ft well? 41 The bucket in Problem 40 is leaking water a.t the rate of 1/10 lb/sec and is raised from the well bottom at the rate of 4ft/sec. How much work is expended in lifting the bucket? 42 Two electrons repel each other with a force inversely proportional to the square of the distance between them, F = k/s2. If one electron is held fixed at the origin, find the work required to move a second electron along the x-axis from the point (10,0) to the point (5,0). 43 If one electron is held fixed at the point (0,0) and another at the point (100,0), find the work required to move a third electron along the x-axis from (50,0) to (80,0).
|
|
Home  Applications of the Integral Applications of the Integral  Some Applications to Physics Some Applications to Physics  Problems Problems |
|
Last Update: 2006-11-25


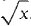 .
.
 , with density equal to the cube of the distance from the y-axis.
, with density equal to the cube of the distance from the y-axis.