Improper Integrals

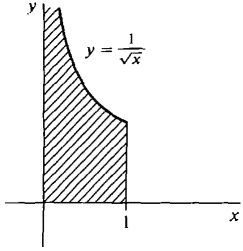
What is the area of the region under the curve y = 1/√x from x = 0 to x = 1 (Figure 6.7.1(a))?

Figure 6.7.1(a)

The function 1/√x is not continuous at x = 0, and in fact 1/√e is infinite for infinitesimal e > 0. Thus our notion of a definite integral does not apply. Nevertheless we shall be able to assign an area to the region using improper integrals. We see from the figure that the region extends infinitely far up in the vertical direction. However, it becomes so thin that the area of the region turns out to be finite.

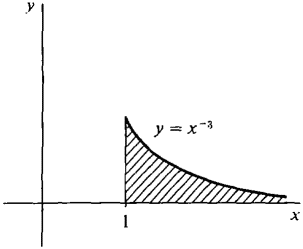
Figure 6.7.1(b)

The region of Figure 6.7.1(b) under the curve y = x^-3 from x = 1 to x = ∞ extends infinitely far in the horizontal direction. We shall see that this region, too, has a finite area which is given by an improper integral.