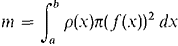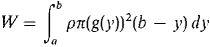| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Extra Problems for Chapter 6 Extra Problems for Chapter 6 |
|






|
|
Extra Problems for Chapter 6
1 The skin is peeled off a spherical apple in four pieces in such a way that each horizontal cross section is a square whose corners are on the original surface of the apple. If the original apple had radius r, find the volume of the peeled apple. 2 Find the volume of a tetrahedron of height h and base a right triangle with legs of length a and b. 3 Find the volume of the wedge formed by cutting a right circular cylinder of radius r with two planes, meeting on a line crossing the axis, one plane perpendicular to the axis and the other at a 45° angle. 4 Find the volume of a solid whose base is the region between the x-axis and the curve y = 1 - x2, and which intersects each plane perpendicular to the x-axis in a square. In Problems 5-8, the region bounded by the given curves is rotated about (a) the x-axis, (b) the y-axis. Find the volumes of the two solids of revolution. 5 y = 0, y = 6 y = 0, y = x3'2, 0 ≤ x ≤ 1 7 y = x, y = 4 - x, 0 ≤ x ≤ 2 8 y = xp, y = xq, 0 ≤ x ≤ 1, where 0 < q < p 9 The region under the curve y = 10 The region under the curve y = (x2 + 4)1/3, 0 ≤ x ≤ 2, is rotated about the y-axis. Find the volume of the solid of revolution. 11 Find the length of the curve y = (2x + 1)3/2, 0 ≤ x ≤ 2. 12 Find the length of the curve y = 3x - 2, 0 ≤ x ≤ 4. 13 Find the length of the curve x = 3t + 1, y = 2 - 4t, 0 ≤ t ≤ 1. 14 Find the length of the curve x = f(t), y = f(t) + c, a ≤ t ≤ b. 15 Find the length of the line x = At + B, y = Ct + D, a ≤ t ≤ b. 16 Find the area of the surface generated by rotating the curve y = 3x2 - 2, 0 ≤ x ≤ 1, about the y-axis. 17 Find the area of the surface generated by rotating the curve x = At2 + Bt, y = 2At + B, 0 ≤ t ≤ 1, about the x-axis. A > 0, B > 0. 18 Find the average value of f(x) = x/ 19 Find the average value of f(x) = xp, 1 ≤ x ≤ b, p ≠ -1. 20 Find the average distance from the origin of a point on the parabola y = x2, 0 ≤ x ≤ 4, with respect to x. 21 Given that f(x) = xp, 0 ≤ x ≤ 1, pa positive constant, find a point c between 0 and 1 such that f(c) equals the average value of f(x). 22 Find the center of mass of a wire on the x-axis, 0 ≤ x ≤ 2, whose density at a point x is equal to the square of the distance from (x, 0) to (0, 1). 23 Find the center of mass of a length of wire with constant density bent into three line segments covering the top, left, and right edges of the square with vertices (0, 0), (0, 1), (1, 1), (1, 0). 24 Find the center of mass of a plane object bounded by the lines y = 0, y = x, x = 1, with density ρ(x) = 1/x. 25 Find the center of mass of a plane object bounded by the curves x = y2, x = 1, with density ρ(y) = y2. 26 Find the centroid of the triangle bounded by the x- and y-axes and the line ax + by = c, where a, b, and c are positive constants. 27 A spring exerts a force of 10x lbs when stretched a distance x beyond its natural length of 2 ft. Find the work required to stretch the spring from a length of 3 ft to 4 ft. In Problems 28-36, test the improper integral for convergence and evaluate if it converges.
 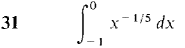 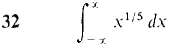 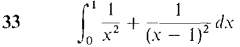  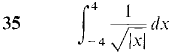 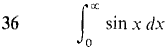 37 A wire has the shape of a curve y = f(x), a ≤ x ≤ b, and has density p(x) at value x. Justify the formulas below for the mass and moments of the wire.
38 Find the mass, moments, and center of mass of a wire bent in the shape of a parabola y = x2, - 1 ≤ x ≤ 1, with density ρ(x) = 39 Find the mass, moments, and center of mass of a wire of constant density ρ bent in the shape of the semicircle y = 40 An object fills the solid generated by rotating the region under the curve y = f(x), a ≤ x ≤ b, about the x-axis. Its density per unit volume is ρ(x). Justify the following formula for the mass of the object.
41 A container filled with water has the shape of a solid of revolution formed by rotating the curve x = g(y), a ≤ y ≤ b, about the (vertical) y-axis. Water has constant density ρ per unit volume. Justify the formula below for the amount of work needed to pump all the water to the top of the container.
42 Find the work needed to pump all the water to the top of a water-filled container in the shape of a cylinder with height h and circular base of radius r. 43 Do Problem 46 if the container is in the shape of a hemispherical bowl of radius r. 44 Do Problem 46 if the container is in the shape of a cone with its vertex at the bottom, height h, and circular top of radius r. 45 The pressure, or force per unit area, exerted by water on the walls of a container is equal to p = ρ(b - y) where ρ is the density of water and b - y the water depth. Find the total force on a dam in the shape of a vertical rectangle of height b and width w, assuming the water comes to the top of the dam. 46 A water-filled container has the shape of a solid formed by rotating the curve x = g(y), a ≤ y ≤ b about the (vertical) y-axis. Justify the formula below for the total force on the walls of the container.
|
|
Home  Applications of the Integral Applications of the Integral  Extra Problems for Chapter 6 Extra Problems for Chapter 6 |
|
Last Update: 2006-11-25


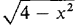 , 0 ≤ x ≤ 1
, 0 ≤ x ≤ 1 , 0 ≤ x ≤ 1, where 0 ≤ p, is rotated about the x-axis. Find the volume of the solid of revolution.
, 0 ≤ x ≤ 1, where 0 ≤ p, is rotated about the x-axis. Find the volume of the solid of revolution. , 0 ≤ x ≤ 4.
, 0 ≤ x ≤ 4.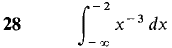

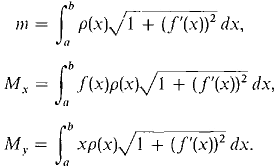

 , -1 ≤ x ≤ 1.
, -1 ≤ x ≤ 1.