The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Trigonometric Functions Trigonometry Theorem 1: Length of Arc
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 1: Length of Arc

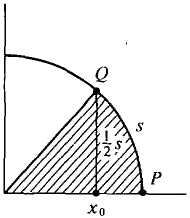
THEOREM 1

Let P be the point P(1, 0).

For every number s between 0 and 2π there is a point Q on the unit circle such that the arc PQ has length s.

PROOF

We give the proof for s between 0 and π/2, whence

0 ≤ h ≤ π/4.

Let A(x) be the area of the sector POQ where Q = Q(x, y) (Figure 7.1.4). Then A(0) = π/4, A(1) = 0 and the function A(x) is continuous for 0 ≤ x ≤ 1. By the Intermediate Value Theorem there is a point x0 between 0 and 1 where the sector has area ½s

A(x0) = ½s.

Therefore the arc PQ has length

2A(x0) = s.

07_trigonometric_functions-5.gif07_trigonometric_functions-6.gif07_trigonometric_functions-7.gif

x = 0, x = x0, x = 1

Figure 7.1.4

Arc lengths are used to measure angles. Two units of measurement for angles are radians (best for mathematics) and degrees (used in everyday life).
Home Trigonometric Functions Trigonometry Theorem 1: Length of Arc

Last Update: 2006-11-05