Definition of Radians

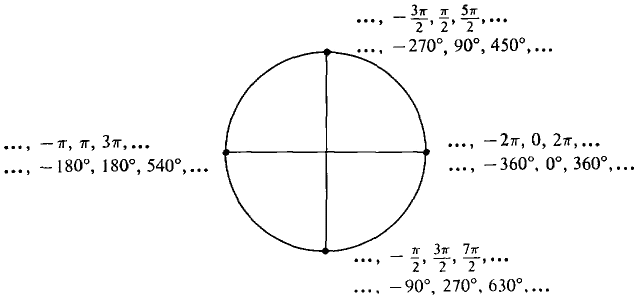
Approximately,

1° ~ 0.01745 radians,

1 radian ~ 57°18' = (57 18/60)°.

A complete revolution is 360° or 2π radians. A straight angle is 180° or π radians. A right angle is 90° or π/2 radians.

It is convenient to take the point (1, 0) as a starting point and measure arc length around the unit circle in a counterclockwise direction. Imagine a particle which moves with speed one counterclockwise around the circle and is at the point (1,0) at time t = 0. It will complete a revolution once every 2% units of time. Thus if the particle is at the point P at time t, it will also be at P at all the times t + 2kn, k an integer. Another way to think of the process is to take a copy of the real line, place the origin at the point (1,0), and wrap the line around the circle infinitely many times with the positive direction going counterclockwise. Then each point on the circle will correspond to an infinite family of real numbers spaced 2n apart (Figure 7.1.5).

Figure7.1.5

The Greek letters θ (theta) and φ (phi) are often used as variables for angles or circular arc lengths.