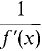| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Trigonometric Functions Trigonometric Functions  Inverse Trigonometric Functions Inverse Trigonometric Functions  Inverse Function Theorem Inverse Function Theorem |
|






|
|
Inverse Function Theorem
We shall next study the derivatives of the inverse trigonometric functions. Here is a general theorem which tells us when the derivative of the inverse function exists and gives a rule for computing its value. INVERSE FUNCTION THEOREM Suppose a real function f is differentiable on an open interval I and f has an inverse function g. Let x be a point in I where f'(x) ≠ 0 and let y = f(x). Then (i) g'(y) exists, (ii) g'(y) = We omit the proof that g'(y) exists. Intuitively, the curve y = f(x) has a non-horizontal tangent line, so the curve x = g(y) should have a nonvertical tangent line and thus g'(y) should exist. The Inverse Function Rule from Chapter 2 says that (ii) is true if we assume (i). The proof of (ii) from (i) is an application of the Chain Rule: g(f(x)) = x, g'(f(x))f'(x) = 1, g'(y)f'(x) = 1, g'(y) = 1/(f'(x)). The Inverse Function Theorem shows that all the inverse trigonometric functions have derivatives. We now evaluate these derivatives.
|
|
Home  Trigonometric Functions Trigonometric Functions  Inverse Trigonometric Functions Inverse Trigonometric Functions  Inverse Function Theorem Inverse Function Theorem |
|
Last Update: 2006-11-05