Inverse Trigonometric Function - Definitions

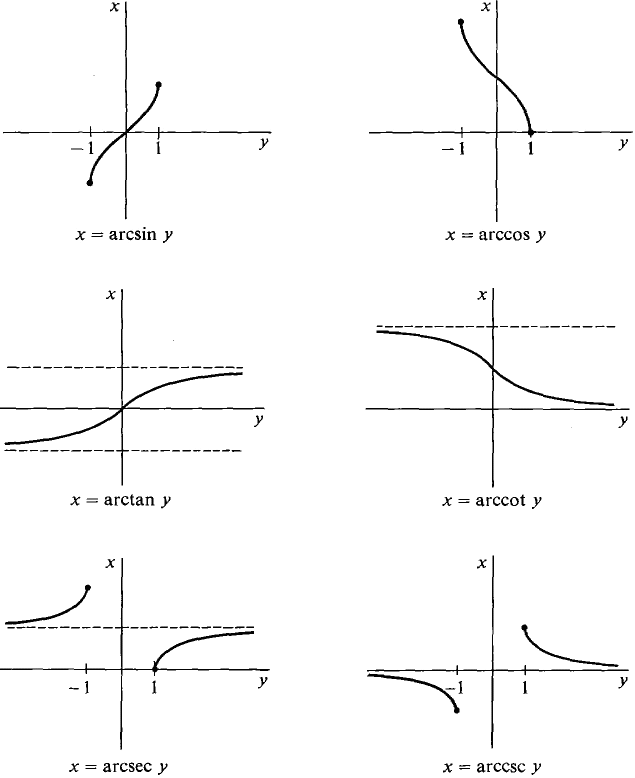
The other trigonometric functions also are not one-to-one and thus do not have inverse functions. However, in each case we obtain a one-to-one function by restricting the domain to a suitable interval, either [ - π/2, π/2] or [0, π]. The resulting inverse functions are called the arccosine, arctangent, etc.

Figure 7.3.5

The graphs of these functions are shown in Figure 7.3.5. The domains of the inverse trigonometric functions can be read off from the graphs, and are shown in the table below.

We can prove the inverse trigonometric functions have these domains (i.e., the figures are correct) using the Intermediate Value Theorem. As an illustration we prove that arcsin y has domain [- 1, 1].

arcsin y is undefined outside [-1,1] because - 1 ≤ sin x ≤ 1 for all x. Suppose y₀ is in [-1, 1]. Then

sin (-π/2) -1 ≤ y₀ ≤ 1 = sin (π/2).

sin x is continuous, so by the Intermediate Value Theorem there exists x₀ between -π/2 and π/2 such that sin x₀ = y₀. Thus

arcsin y₀ = x₀

and y₀ is in the domain of arcsin y.