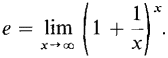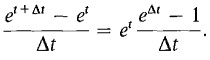| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e |
|||||||||||||






|
|||||||||||||
Derivatives of Exponential Functions and the Number e
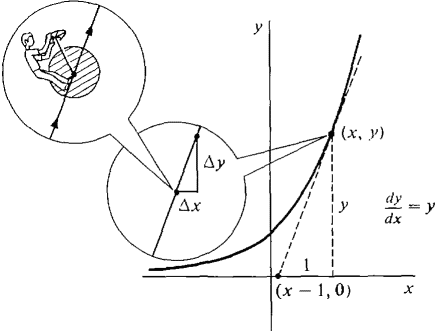
One of the most important constants in mathematics is the number e, whose value is approximately 2.71828. In this section we introduce e and show that it has the following remarkable properties. (1) The function y = ex is equal to its own derivative. (2) e is the limit Either property can be used as the definition of e. Because of property 1, it is convenient in the calculus to use exponential and logarithmic functions with the base e instead of 10. However, it is not at all easy to prove that such a number e exists. Before going into further detail we shall discuss these properties intuitively. A function which equals its own derivative may be described as follows. Imagine a point moving on the (x, y) plane starting at (0, 1). The point is equipped with a little man and a steering wheel which controls the direction of motion of the point. The man always steers directly away from the point (x - 1,0), so that
Then the point will trace out a curve y = f(x) which equals its own derivative, as in Figure 8.3.1.
Figure 8.3.1 Another intuitive description is based on the example of the population growth function y = at. If the birth rate minus the death rate is equal to one, then the derivative of at is at, and a is the constant e. Imagine a country with one million people (one unit of population) at time f = 0 which has an annual birth rate of one million births per million people, and zero death rate. Then after one year the population will be approximately e million, or 2,718,282. (This high a growth rate is not recommended.) The limit e = limx→∞ (1 + 1/x)x is suggested intuitively by the notion of continuously compounded interest. Suppose a bank gives interest at the annual rate of 100%, and we deposit one dollar in an account at time t = 0. If the interest is compounded annually, then after t = 1 year our account will have 2 dollars. If the interest is compounded quarterly (four times per year), then our account will grow to 1 + ¼ dollars at time t = ¼, (1 + ¼)2 dollars at time t = j, and so on. After one year our account will have (1 + ¼)4 ~ 2.44 dollars. Similarly, if our account is compounded daily then after one year it will have (1 + 1/365)365 dollars, and if it is compounded n times per year it will have (1 + 1/n)n dollars after one year. Table 8.3.1 shows the value of (1 + 1/n)n for various values of n. (The last few values can be found with some hand calculators.) Table 8.3.1
This table strongly suggests that the limit e = limx→∞ (1 + 1/x)x exists. A proof will be given later. Thus for H positive infinite,
If the interest is compounded H times per year, then in t years each dollar will grow to
Thus if the 100% interest is continuously compounded, each dollar in the account grows to et dollars in t years. At the interest rate r, each dollar in a continuously compounded account will grow to ert dollars in t years. For more information, see Section 8.4. We now turn to a detailed discussion of e. LEMMA The limit We shall save the proof of this lemma for the end of the section. DEFINITION
As we have indicated before, e has the approximate value e ~ 2.71828. The function y = ex is called the exponential function and is sometimes written y = exp x. THEOREM 1 e is the unique real number such that
PROOF Our plan is to show that whenever t and t + Δt are finite and differ by a nonzero infinitesimal Δt,
We may assume that t is the smaller of the two numbers, so that Δt is positive. By the rules of exponents, (1) Let (2) Then
Since ex is continuous and e0 = 1, we see from Equation 2 that b Δt is positive infinitesimal. Thus H = 1/b Δt is positive infinite. From Equation 2,
Taking standard parts,
Therefore st(b) = 1, and by Equation 1,
We conclude that for real x,
It remains to prove that e is the only real number with this property. Let a be any positive real number different from e, a ≠ e. We may then differentiate ax by the Chain Rule.
Since a ≠ e, loge a ≠ 1, so (d(ax))/dx ≠ ax. Since ex is its own derivative, it is also its own antiderivative. We thus have a new differentiation formula and a new integration formula which should be memorized.
We are now ready to plot the graph of the exponential curve y = ex. Here is a short table. It gives both the value y and the slope y', because y = y' = ex.
The number ex is always positive, and y, y', and y" all equal ex. From this we can draw three conclusions.
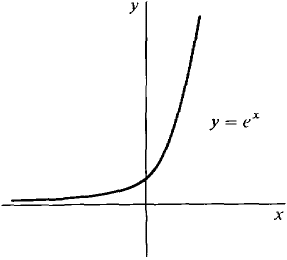
If H is positive infinite, then by Rule (vii), eH ≥ 1 + H(e - 1). So eH is infinite, e-H = 1/eH is infinitesimal. Therefore, limx→∞ ex = ∞, limx→-∞ ex = 0. We use this information to draw the curve in Figure 8.3.2.
Figure 8.3.2
|
|||||||||||||
Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e |
|||||||||||||
Last Update: 2010-11-25



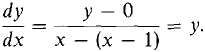
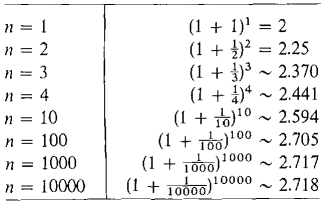

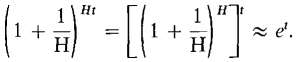
 exists.
exists.