| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e  Geometric Series Formula - Proof of Lemma Geometric Series Formula - Proof of Lemma |
|






|
|
Geometric Series Formula - Proof of Lemma
We conclude this section with the proof of the lemma that limx→∞ (1 + 1/x)x exists. We use the following formula from elementary algebra. GEOMETRIC SERIES FORMULA If b ≠ 1, then
This formula is proved by multiplying (1 + b + b2 + ... + bn)(b - 1) = (b + b2 + ... + bn + bn+1) - (1 + b + ... + bn-1 + bn) = bnn+1 - 1. PROOF OF THE LEMMA The function y = 2t is continuous and positive. Therefore the integral
is a positive real number. Our plan is to use the fact that the Riemann sums approach c to show that (1 + 1/x)x approaches the limit 2c. Let H be positive infinite. We wish to prove that
It is easier to work with the logarithm
Let
Δt is positive and is infinitesimal because Δt ≈ log2 1 = 0. Moreover, so (3)
Let us form the Riemann sum
For simplicity suppose Δt evenly divides 1, so K Δt = 1. By the Geometric Series Formula,
By Equation 3,
Taking standard parts we have
Finally,
The proof is the same when Δt does not evenly divide 1, except that K Δt is infinitely close to 1 instead of equal to 1. Therefore
We remark that in the above proof we could have used any other positive real number in place of 2. Notice that 2c = e, so the constant
|
|
Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Derivatives of Exponential Functions and the Number e Derivatives of Exponential Functions and the Number e  Geometric Series Formula - Proof of Lemma Geometric Series Formula - Proof of Lemma |
|
Last Update: 2010-11-25


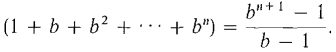
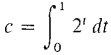
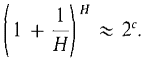

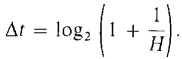
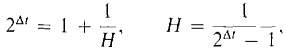
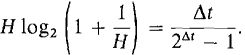

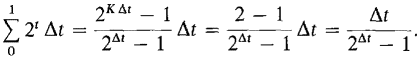

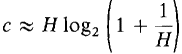

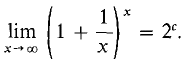
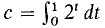 is just log2 e.
is just log2 e.