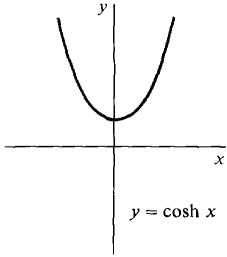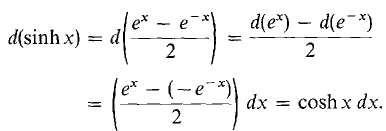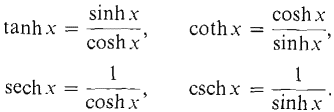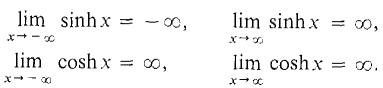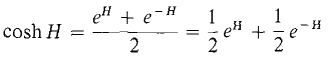Hyperbolic Functions

In this section we shall discuss some functions involving exponentials which come up in physical and social sciences.

The hyperbolic functions are analogous to the trigonometric functions and are useful in physics and engineering.

The hyperbolic sine, sinh, and the hyperbolic cosine, cosh, are defined as follows.

A chain fixed at both ends will hang in the shape of the curve y = cosh x (the catenary). The graphs of y = sinh x and y = cosh x are shown in Figure 8.4.1.

Figure 8.4.1

The hyperbolic functions have identities which are similar to, but different from, the trigonometric identities. We list some of them in Table 8.4.1.

These hyperbolic identities are easily verified. For example,

Notice that

When we multiply these we get the identity

cosh² x - sinh² x = 1.

The other hyperbolic functions are defined like the other trigonometric functions,

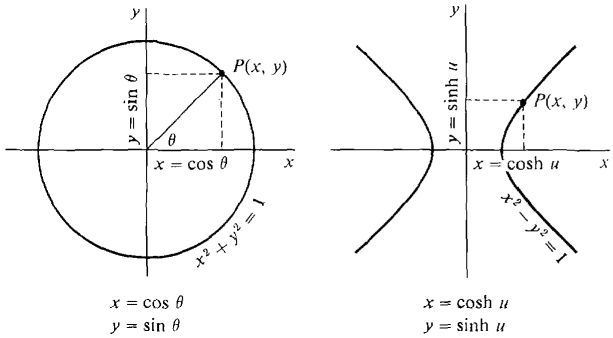
The hyperbolic functions are related to the unit hyperbola x² - y² = 1 in the same way that the trigonometric functions are related to the unit circle x² + y² = 1 (Figure 8.4.2).

Figure 8.4.2

If we put

x = cos θ, y = sin θ,

we have

x² + y² = cos² θ + sin² θ = 1,

so the point P(x, y) is on the unit circle x² + y² = 1. On the other hand if we put x = cosh u, y = sinh u, we have

x² - y² = cosh² u - sinh² u = 1,

so the point P(x, y) is on the unit hyperbola x² - y² = 1.

The hyperbolic functions differ from the trigonometric functions in some important ways. The most striking difference is that the hyperbolic functions are not periodic. In fact both sinh x and cosh x have infinite limits as x becomes infinite:

Let us verify the last limit. If if is positive infinite, then

is the sum of a positive infinite number ½ e^H and an infinitesimal ½ e^-H and hence is positive infinite. Therefore lim_x→∞ cosh x = ∞.