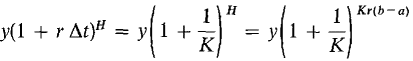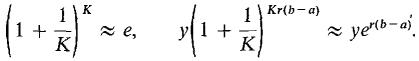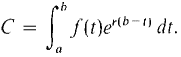Application to Economics

We now give an application of the exponential function to economics. Suppose money in the bank earns interest at the annual rate r, compounded continuously. (To keep our problem simple we assume r is constant with time, even though actual interest rates fluctuate with time.) Here is the problem: A person receives money continuously at the rate of f(t) dollars per year and puts the money in the bank as he receives it. How much money will be accumulated during the time a ≤ t ≤ b? This is an integration problem.

We first consider a simpler problem. If a person puts y dollars in the bank at time t = a, how much will he have at time t = b? The answer is

ye^r(b-a) dollars.

JUSTIFICATION

Divide the time interval [a,b] into subintervals of infinitesimal length Δt > 0,

a, a + Δt, a + 2 Δt, ..., a + H Δt = b, where Δt = (b - a)/H.

If the interest is compounded at time intervals of Δt, the account at the above times will be

y, y(1 + r Δt), y(1 + r Δt)², ..., y(1 + r Δt)H.

Let K = 1/(r Δt).

Then

H = (b - a)/Δt = r(b - a)K.

At time b the account is

Since H, and hence K, is positive infinite,

Thus when the interest is compounded infinitely often the account at time b is infinitely close to ye^r(b-a). So when the interest is compounded continuously the account at time b is

ye^r(b-a)

Now we return to the original problem.

CAPITAL ACCUMULATION FORMULA

If money is received continuously at the rate of f(t) dollars per year and earns interest at the annual rate r, the amount of capital accumulated between times t = a and t = b is

JUSTIFICATION

During an infinitesimal time interval [r, t + Δt], of length Δt, the amount received is

Δy ≈ f(t) Δt (compared to Δf).

This amount Δy will earn interest from time t to b, so its contribution to the total capital at time b will be

ΔC ≈ Δye^r(b-t) = f(t)e^r(b-t) Δt (compared to Δt).

Therefore by the Infinite Sum Theorem, the total capital accumulated from t = a to f = b is the integral