Positive Term Series - Theorem 1

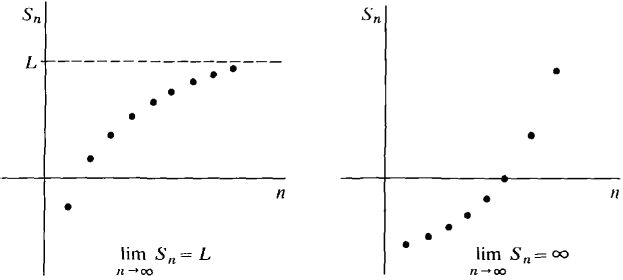
9.4 SERIES WITH POSITIVE TERMS

By a positive term series, we mean a series in which every term is greater than zero. For example, the geometric series

1 + c + c² + ... + cⁿ + ...

is a positive term series if c > 0 but not if c ≤ 0. We call a sequence S₁, S₂, ..., S_n, ... increasing if S_m < S_n whenever m < n. It is easy to see that

a_t + a₂ + ... + a_n + ...

is a positive term series if and only if its partial sum sequence is increasing. We are going to give several tests for the convergence of a positive term series. The starting point is the following theorem.

Geometrically, this says that, as n gets large, the graph of the sequence either levels out at a limit L or the value of S_n gets large (Figure 9.4.1). We omit the proof. (The proof is given in the Epilogue at the end of the book.)

Figure 9.4.1

Theorem 1 has an equivalent form for positive term series because the partial sum sequence of a positive term series is increasing.

Example 1: Harmonic Series Diverges to ∞

Example 2: Geometric Series

Remark: Theorem 1 shows that to determine whether a positive term series converges, we need only look at one infinite partial sum. If it is finite the series converges and if it is infinite the series diverges to ∞.