| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Comparison Test Comparison Test |
|||||






|
|||||
Comparison Test
COMPARISON TEST Let c be a positive constant. Suppose series and an ≤ cbn for all n. (i) If (ii) If PROOF (i) Suppose Each finite partial sum of
Therefore, an infinite partial sum It follows that (ii) If To use the Comparison Test we compare a series whose convergence or divergence is unknown with one which is known.
The harmonic series Sometimes the following comparison test is easier to use.
|
|||||
Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Comparison Test Comparison Test |
|||||
Last Update: 2006-11-07


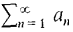 and
and 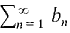 are positive term
are positive term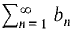 converges then
converges then 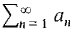 converges.
converges. diverges then
diverges then 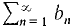 diverges.
diverges.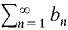 converges to S. The Constant Rule gives
converges to S. The Constant Rule gives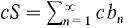
 is less than cS,
is less than cS,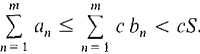
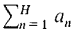 is less than cS and hence finite.
is less than cS and hence finite. converges.
converges.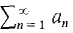 diverges then
diverges then 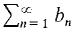 cannot converge by part (i).
cannot converge by part (i).
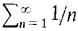 diverges, whence the given series diverges.
diverges, whence the given series diverges.