| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Theorem 2: Integral Test. Theorem 2: Integral Test. |
|






|
|
Theorem 2: Integral Test.
For our last test we need another theorem which is similar to Theorem 1. THEOREM 2 If the function F(x) increases for x ≥ 1, then limx→∞ F(x) either exists or is infinite. This says that the curve y - F(x) is either asymptotic to some horizontal line y = L or increases indefinitely, as illustrated in Figure 9.4.2. 
Figure 9.4.2 INTEGRAL TEST Suppose f is a continuous decreasing function and f(x) > 0 for all x ≥ 1. Then the improper integral
and the infinite series
either both converge or both diverge to ∞. Discussion Figure 9.4.3 suggests that
so the series and the integral should both converge or both diverge to ∞. The Integral Test shows that the integral have the same convergence properties. However, their values, when finite, are different. In fact, we can see from Figure 9.4.3(c) that the integral is less than the series sum,
Figure 9.4.3 The Integral Test PROOF As we can see from Figure 9.4.3, for each m we have
The improper integral is defined by
Since f(x) is always positive, the function Case 1
Case 2
|
|
Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Theorem 2: Integral Test. Theorem 2: Integral Test. |
|
Last Update: 2006-11-07


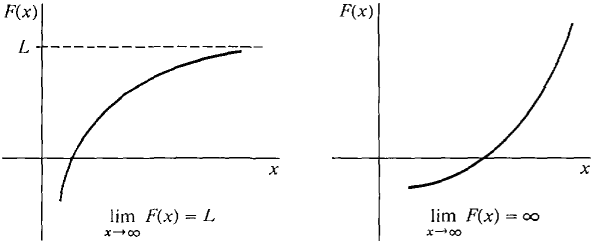


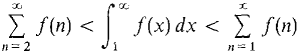
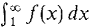 and the series
and the series 
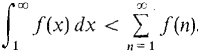
 (a)
(a)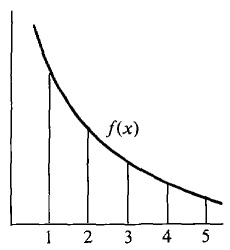 (b)
(b)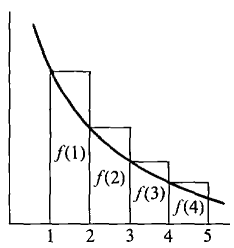 (c)
(c)
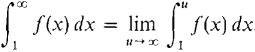
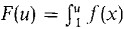 dx is increasing, so by Theorem 2, the limit either exists or is infinite. Hence the improper integral either converges or diverges to ∞.
dx is increasing, so by Theorem 2, the limit either exists or is infinite. Hence the improper integral either converges or diverges to ∞.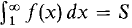 converges.
converges. 
 and the series
and the series converge.
converge.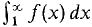 diverges to ∞.
diverges to ∞.  , the infinite partial
, the infinite partial diverges to ∞.
diverges to ∞.