| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Limit Comparison Test Limit Comparison Test |
|||






|
|||
Limit Comparison Test
LIMIT COMPARISON TEST Let Suppose that aK ≤ cbK for all infinite K. Then:
PROOF Assume bH+1 + bH+2 + ... + bK ≈ 0. Hence 0 ≤ aH+1 + ... + aK ≤ cbH+1 + ... + cbK = c(bH+1 + ... + bK) ≈ 0. It follows that aH+1 + ... + aK ≈ 0 and
|
|||
Home  Infinite Series Infinite Series  Series With Positive Terms Series With Positive Terms  Limit Comparison Test Limit Comparison Test |
|||
Last Update: 2006-11-07


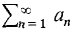 and
and be positive term series and c a positive real number.
be positive term series and c a positive real number. converges then
converges then  converges.
converges.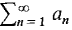 diverges then
diverges then  diverges.
diverges.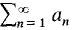 converges.
converges.