| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Power series Power series  Definition of Power Series Definition of Power Series |
|






|
|
Definition of Power Series
9.7 POWER SERIES So far we have studied series of constants,
One can also form a series of functions
Such a series will converge for some values of x and diverge for others. The sum of the series is a new function
which is defined at each point x0 where the series converges. We shall concentrate on a particular kind of series of functions called a power series. Its importance will be evident in the next section where we show that many familiar functions are sums of power series. DEFINITION A power series in x is a series of functions of the form
The nth finite partial sum of a power series is just a polynomial of degree n,
The infinite partial sums are polynomials of infinite degree,
At x = 0 every power series converges absolutely,
(In a power series we use the convention a0x0 = a0.) If a power series converges absolutely at x = u, it also converges absolutely at x = -u, because the absolute value series Intuitively, the smaller the absolute value |x|, the more likely the power series is to converge at x. This intuition is borne out in the following theorem.
|
|
Home  Infinite Series Infinite Series  Power series Power series  Definition of Power Series Definition of Power Series |
|
Last Update: 2006-11-08






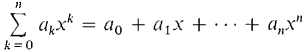


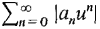 and
and  are the same.
are the same.