| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Mean Value Theorem and Taylors Formula Mean Value Theorem and Taylors Formula |
|






|
|
Mean Value Theorem and Taylors Formula
We can easily find the Taylor polynomials of f(x) by differentiating. Let us now try to find a formula for the Taylor remainders. The Mean Value Theorem gives a formula for the Taylor remainder, R0(x). MEAN VALUE THEOREM (Repeated) Suppose f(t) is differentiate at all t between c and d. Then
for some point t0 strictly between c and d. When we replace d by x, this gives the formula f(x) = f(c) + R0(x). R0(x) = f'(t0)(x - c). Taylor's Formula is a generalization of the Mean Value Theorem which gives the nth Taylor remainder. TAYLOR'S FORMULA Suppose the (n + l)st derivative f(n+1)(t) exists for all t between c and x. Then f(x) = f(c) + f'(c)(x - c) + where Rn(x) = for some point tn strictly between c and x. Notice that the remainder term looks just like the (n + 1)st term of a Taylor polynomial except that f(n+1)(c) is replaced by f(n+1)(tn). When r = 0 Taylor's Formula is sometimes called MacLaurin's Formula. Taylor's Formula can be used to get an estimate of the error Rn(x) between f(x) and the Taylor polynomial Pn(x). For example if |f(n+1)(t)| ≤ Mn+1 for all t between c and x. then we obtain the error estimate |Rn(x)| ≤ Taylor polynomials with the error estimate are of great practical value in obtaining approximations. In the next example we use Taylor's Formula to approximate the value of e.
|
|
Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Mean Value Theorem and Taylors Formula Mean Value Theorem and Taylors Formula |
|
Last Update: 2006-11-08


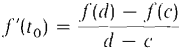
 (x - c)2 + ... +
(x - c)2 + ... +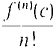 (x - c)n + Rn(x)
(x - c)n + Rn(x)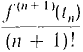 (x - c)n+1
(x - c)n+1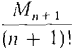 |x - c|(n+1).
|x - c|(n+1).