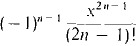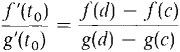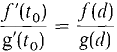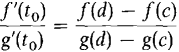| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Infinite Series Taylor's Formula Generalized Mean Value Theorem |
|||||||||||||||||
 Search the VIAS Library | Index
|
  |
||||||||||||||||
Generalized Mean Value Theorem
MacLaurin's Formula can be used to approximate sin x (with x in radians) when x is close to zero. We approximate sin (18°) as follows. x = 18° = π/10 ~ 0.31415927 radians.
Thus sin (18°) ~ 0.3090171 to seven places. The proof of Taylor's Formula uses the following generalized form of the Mean Value Theorem. GENERALIZED MEAN VALUE THEOREM Suppose f and g are differentiate at all t between c and d, and that g'(t) ≠ 0 for t strictly between c and d. Then
for some point t0 strictly between c and d. This theorem can be illustrated graphically by plotting the parametric equations x = g(t), y = f(t) in the (x, y) plane, as in Figure 9.10.3.
Figure 9.10.3 If f(c) = 0 and g(c) = 0, the formula in the theorem takes on the simpler form
This is the form which will be used in the proof of Taylor's Formula.
PROOF OF THE GENERALIZED MEAN VALUE THEOREM Introduce the new function h(t) = f(t)(g(d) - g(c)) - g(t)(f(d) - f(c)). Then h(t) is also differentiable at all points between c and d. Furthermore, at the endpoints c and d we have h(c) = f(c)g(d) - f(d)g(c) = h(d). We may therefore apply Rolle's Theorem, whence there is a point t0 strictly between c and d such that h'(t0) = 0. Differentiating h(t), we get h'W = f'(t)(g(d) - g(c)) - g'(t)(f(d) - f(c)). Therefore at t = t0, 0 = f'(t0)(g(d) - g(c)) - g'(t0)(f(d) - f(c)). g'(t) is never zero. Also, g(c) ≠ g(d) because otherwise Rolle's Theorem would give a t with g'(i) = 0. We may therefore divide out and obtain the desired formula
|
|||||||||||||||||
| Home Infinite Series Taylor's Formula Generalized Mean Value Theorem |
|
||||||||||||||||
Last Update: 2006-11-08