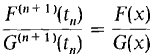| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Proof Of Taylor's Formula Proof Of Taylor's Formula |
|






|
|
Proof Of Taylor's Formula
PROOF OF TAYLOR'S FORMULA Let F(x) = Rn(x), G(x) = (x - c)n+1. Then F(x) = f(x) - Pn(x). f(x) and the nth Taylor polynomial Pn(x) have the same value and first n derivatives at x = c. Therefore F(c) = F'(c) = F"(c) = ... = F(n)(c) = 0. We also see that G(c) = G(c) = G"(c) = ... = G(n)(c) = 0. Using the Generalized Mean Value Theorem n + 1 times, we have
It follows that
Either x < t0 < t1 < ... < tn < c or x > t0 > t1 > ... > tn > c, so tn is strictly between c and x. The (n + l)st derivatives of F(t) and G(t) are f(n+1)(t) = f(n+1)(t) - 0, G(n+1)(t) = (n + 1)! Substituting, we have
and Taylor's Formula follows at once.
|
|
Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Proof Of Taylor's Formula Proof Of Taylor's Formula |
|
Last Update: 2006-11-08


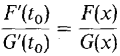 for some t0 strictly between c and x;
for some t0 strictly between c and x; for some t1 strictly between c and t0;
for some t1 strictly between c and t0;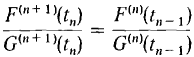 for some tn strictly between c and tn-1.
for some tn strictly between c and tn-1.