| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Taylor Series Taylor Series  Review of Power Series (MacLaurin Series) Review of Power Series (MacLaurin Series) |
|||






|
|||
Review of Power Series (MacLaurin Series)
Here is a review of the power series obtained earlier in this chapter. By Theorem 1, they are all MacLaurin series. (1) (2) (3) (4) (5) (6) (7) (9) (11) (13) (14) At the end of this section we shall add three important power series to our list: (15) (16) (17) where p is constant. The last series is called the binomial series. It is interesting to observe that the derivatives of an analytic function at zero can be read directly from the MacLaurin series. Sometimes it is quite hard to compute the derivative directly but easy to take it from the MacLaurin series.
|
|||
Home  Infinite Series Infinite Series  Taylor Series Taylor Series  Review of Power Series (MacLaurin Series) Review of Power Series (MacLaurin Series) |
|||
Last Update: 2006-11-08


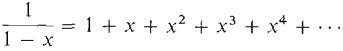 , |x| < 1
, |x| < 1 , |x| < 1
, |x| < 1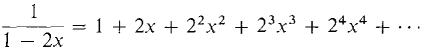 , |x| < ½
, |x| < ½ , |x|< 1
, |x|< 1 , |x| < 1
, |x| < 1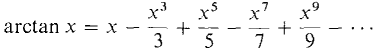 , |x| < 1
, |x| < 1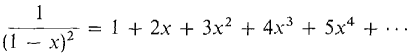 , |x| < 1 (8)
, |x| < 1 (8)
 (10)
(10)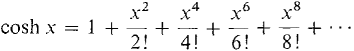
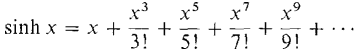 (12)
(12)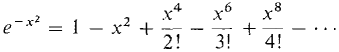

 , |x| < 1
, |x| < 1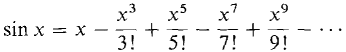

 , |x| < 1,
, |x| < 1,