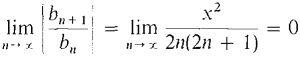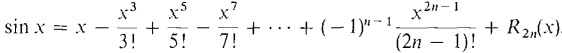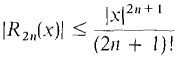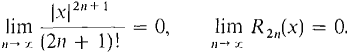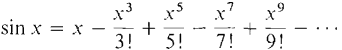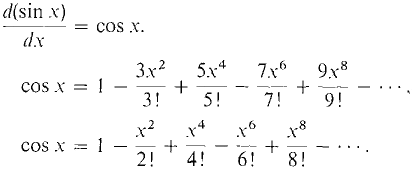| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Taylor Series Taylor Series  Power Series for sin x and cos x Power Series for sin x and cos x |
|||||||






|
|||||||
Power Series for sin x and cos x
Suppose we are given a function f(x) and a point c, and we wish to represent f(x) as the sum of a power series in x - c. This will be possible for some functions (the analytic functions), but not for all. Theorem 1 shows that if there is such a power series it is the Taylor series for f(x). Thus we use the following steps to represent f(x) as a power series. Step 1 Compute all the derivatives f(n)(c), n = 0,1, 2,.... If these derivatives do not all exist, f(x) is not the sum of a power series in powers of x - c. Step 2 Write down the Taylor series of f(x) at x = c and find its radius of convergence r. Step 3 If possible, show that f(x) is equal to the sum of its Taylor series for c - r < x < c + r. We shall now use Steps 1-3 to obtain the power series for sin x, cos x, and (1 + x)p. THE POWER SERIES FOR sin x
Conclusion: Since the remainders approach zero, the MacLaurin polynomials approach sin x. So for all x,
THE POWER SERIES FOR cos xThis power series can be found by the same method as was used for sin x. However, it is simpler to differentiate the power series for sin x.
|
|||||||
Home  Infinite Series Infinite Series  Taylor Series Taylor Series  Power Series for sin x and cos x Power Series for sin x and cos x |
|||||||
Last Update: 2006-11-08



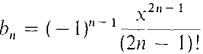 . We use the Ratio Test,
. We use the Ratio Test,