Elementary Calculus: Binomial Series

The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home

Infinite Series

Taylor Series

Binomial Series

Search the VIAS Library | Index

Binomial Series

THE BINOMIAL SERIES FOR (1+x)^p

Let us first consider the case where p is a nonnegative integer m, whence (1 + x)^m is a polynomial. The Binomial Theorem states that for nonnegative integers m,

Setting a = 1 and b = x we obtain a finite power series for (f + x)^m,

When p < 0, and when p > 0 but p is not an integer, we shall see that (1 + x)^pis the sum of a similar power series but with infinitely many terms. Let g(x) = (1 + x)^p.

Step 1

By differentiation we see that

g'(x) = p(i + x^)p-1g"(x) = p (p - 1)(1 + x)^p-2,

g⁽ⁿ⁾(x) = p (p - 1) ... (p - n + 1)(1 + x)^p-n.

Thus at x = 0, g(0) = 1, g'(0) = p, g"(0) = p (p - 1), g⁽ⁿ⁾(0) = p(p - l)...(p - n + 1).

Step 2

The MacLaurin series is

We use the Ratio Test.

Therefore the series converges for |x| < 1, diverges for |x| > 1, and has radius of convergence r = 1. We denote the sum by f(x).

Step 3

We wish to show that the sum f(x) is equal to (1 +x)^pfor|x| < 1. In this case, the MacLaurin Formula does not give the needed information (see Problem 27 at the end of this section). Instead we show that the quotient f(x)/(l + x)^phas derivative zero for |x| < 1. We have

It suffices to show that f'(x)(1 + x) = pf(x) or f'(x) + xf'(x) = pf(x). Let us compute f'(x) and xf'(x).

Adding the power series, we have

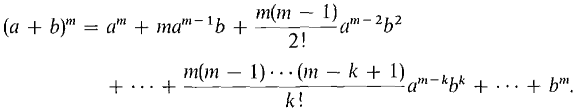
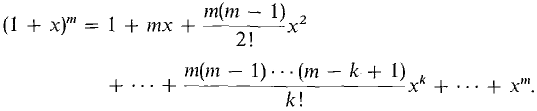
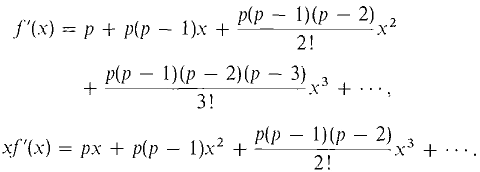
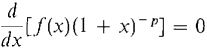Thus f'(x) + xf'(x) = pf(x), We conclude that for some constant C, f(x)(l + x)^-p = C.

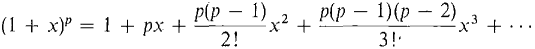At x = 0, f(x) = 1 = (1 + x)^-p. Hence C = 1. This shows that (1 + x)^p = f(x) for |x| < 1. Thus we have the binomial series

|x| < 1.

Home

Infinite Series

Taylor Series

Binomial Series

Last Update: 2006-11-08