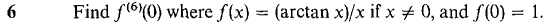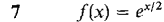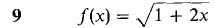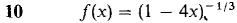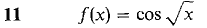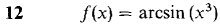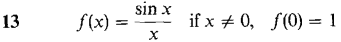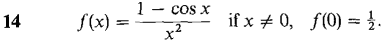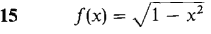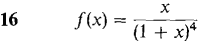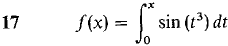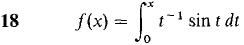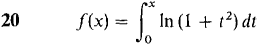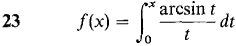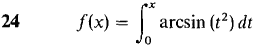Problems

In Problems 7-24, find a power series converging to f(x) and determine the radius of convergence.

25            Find the Taylor series for ln x in powers of x - 1.

26            Find the Taylor series for sin x in powers of x - π/4.

27            Use Taylor's Formula to prove that the binomial series converges to (1 + x)^p when -½ ≤ x < 1. (The proof in the text shows that it actually converges to (1 + x)^p for - 1 < x < 1.)

28            Let  f(x) = 0              if x = 0,

f(x) = e^-1/x² if x ≠ 0,

Show that f⁽ⁿ⁾(0) = 0 for all integers n; so for x ≠ 0 the MacLaurin series converges but to zero instead of to f(x).