| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Extra Problems for Chapter 9 Extra Problems for Chapter 9 |
|






|
|
Extra Problems for Chapter 9
Determine whether the sequences 1-5 converge and find the limits when they exist.
Determine whether the series 6-12 converge and find the sums when they exist.
Test the series 13-23 for convergence.
Test the series 27-30 by the Ratio Test.
Find the radius of convergence of the power series in Problems 31-35.
36 Find the interval of convergence of 37 Find the power series and radius of convergence for f'(x) and
38 Find a power series for f(x) = 1/(1 + 2x3) and determine its radius of convergence. 39 Find a power series for
and determine its radius of convergence. 40 Approximate 41 Approximate 42 Approximate 43 Approximate 44 Find a power series for (1 + x3)-3/2 and give its radius of convergence. 45 Find a power series for 46 Prove that any repeating decimal 0.b1b2...bnb1b2...bnb1b2...bn... (where each of b1, ..., bn is a digit from the set {0,1,..., 9}) is equal to a rational number. 47 Approximately how many terms of the harmonic series 1 + ½ + ⅓ + ... + l/n + ... are needed to reach a partial sum of at least 50? Hint: Compare with 48 Suppose 49 Suppose
finite partial sum of and vice versa. 50 Give a rearrangement of the series 1 - ½ + ⅓ - ¼ + ... which diverges to - x. 51 Suppose 52 Prove the following result using the Limit Comparison Test. Let
53 Multiplication of Power Series. Prove that if f(x) = Hint: First prove the corresponding formula for partial sums, then take the standard part of an infinite partial sum. 54 Suppose f(x) is the sum of a power series for |x| < r and let g(x) = f(x2). Prove that for each n,
55 Show that if p ≤ -1 then the binomial series
diverges at x = 1 and x = -1. Hint: Cauchy Test. If p ≥ 1, the series converges at x = 1 and x = -1. Hint: Compare with 56 Prove that e is irrational, that is, e ≠ a/b for all integers a, b. Hint: Suppose e = a/b, e-1 = b/a. Let
|
|
Home  Infinite Series Infinite Series  Extra Problems for Chapter 9 Extra Problems for Chapter 9 |
|
Last Update: 2006-11-25



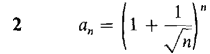

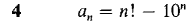




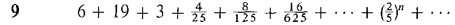


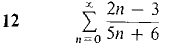

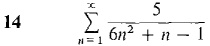
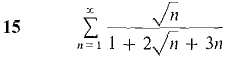

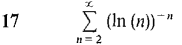
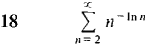

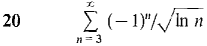
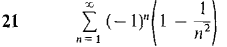




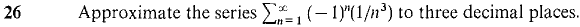


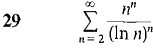
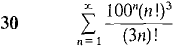


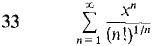


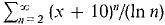
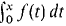 where
where
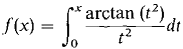
 within 0.0001.
within 0.0001. within 0.001.
within 0.001.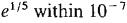
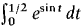 within 0.01.
within 0.01. and determine its radius of convergence.
and determine its radius of convergence.
 and
and  is either finite or ∞. Prove that
is either finite or ∞. Prove that 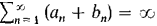
 is a convergent positive term series and
is a convergent positive term series and  is a rearrangement of
is a rearrangement of . Prove that
. Prove that 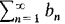 converges and has the same sum. Hint: Show that each
converges and has the same sum. Hint: Show that each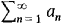 is less than or equal to each infinite partial sum of
is less than or equal to each infinite partial sum of 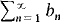 ,
, , and an≤ cn≤ bn for all n. Prove that
, and an≤ cn≤ bn for all n. Prove that 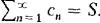
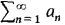 and
and  be positive term series and suppose limn→∞ (an/bn) exists. If
be positive term series and suppose limn→∞ (an/bn) exists. If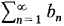 converges then
converges then  converges. If
converges. If  diverges then
diverges then  diverges.
diverges. and g(x) =
and g(x) = then f(x)g(x) =
then f(x)g(x) =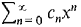 where cn = a0bn + a1 bn-1 + ... + an-1b1 + anb0.
where cn = a0bn + a1 bn-1 + ... + an-1b1 + anb0.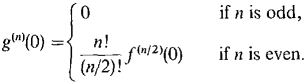
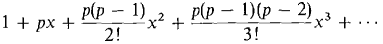
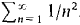 Note: The cases -1 < p < 1 are more difficult. It turns out that if -1 < p < 0 the series converges at x = 1 and diverges at x= -1. If p ≥ 0 the series converges at x = 1 and x = -1.
Note: The cases -1 < p < 1 are more difficult. It turns out that if -1 < p < 0 the series converges at x = 1 and diverges at x= -1. If p ≥ 0 the series converges at x = 1 and x = -1. . Then |c| ≥ 1/a! but |c| ≤ l/(a +1)!.
. Then |c| ≥ 1/a! but |c| ≤ l/(a +1)!.