| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vectors Vectors  Vector Algebra Vector Algebra  Vector Sums - Theorem 1 Vector Sums - Theorem 1 |
|






|
|
Vector Sums - Theorem 1
The sum A + B of vectors A and B is defined as follows. Let
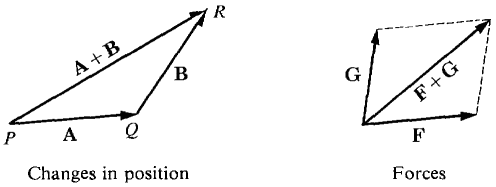
Figure 10.1.6 Sum of Two Vectors If an object in the plane originally has the position vector P and is moved by a displacement vector D, its new position vector will be the vector sum P + D. If an object is moved twice, first by a displacement vector D and then by a displacement vector E, the total displacement vector is the sum D + E. If two forces F and G are acting simultaneously on an object, their combined effect is the vector sum F + G (Figure 10.1.7). The combined effect of three or more forces acting on an object is also the vector sum, e.g., (F + G) + H. Newton's first law of motion states that if an object is at rest, the vector sum of all forces acting on the object is the zero vector.
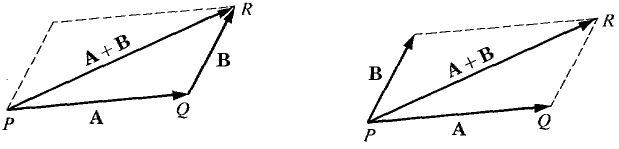
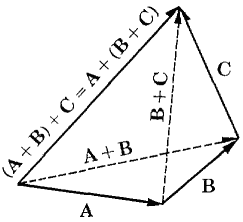
Figure 10.1.7 In economics, if a trader initially has a commodity vector A and buys a commodity vector B (i.e., he buys a quantity b1 of commodity one and b2 of commodity two), his new commodity vector will be the vector sum A + B. The vector sum is also useful in discussing an exchange between two or more traders. Suppose traders A and B initially have commodity vectors A1 and B1. After exchanging goods, they have new commodity vectors A2 and B2. Since the total amount of each good remains unchanged, we see that A1 + B1 = A2 + B2. Vector sums obey rules similar to the rules for sums of real numbers.THEOREM 1 Let A, B, ami C be vectors. (i) Identity Law A + 0 = 0 + A = A. (ii) Commutative Law A + B = B + A. (iii) Associative Law (A + B) + C = A + (B + C). (iv) Triangle Inequality |A + B| ≤ |A| + |B|. We shall skip the proofs, which use the corresponding laws for real numbers. The Commutative and Associative Laws are illustrated by Figure 10.1.8.
Figure 10.1.8a: Associative law
Figure 10.1.8b: Commutative law The Triangle Inequality says that the length of one side of a triangle is at most the sum of the lengths of the other two sides. This is because the vectors A, B, and A + B are represented by sides of a triangle. The proof of the Triangle Inequality is left as a problem (with a hint). It is illustrated in Figure 10.1.9.
Triangle inequality Figure 10.1.9
|
|
Home  Vectors Vectors  Vector Algebra Vector Algebra  Vector Sums - Theorem 1 Vector Sums - Theorem 1 |
|
Last Update: 2006-11-07


 represent
represent 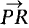 . More briefly, if A is the vector from P to Q and
. More briefly, if A is the vector from P to Q and