| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vectors Vectors  Extra Problems for Chapter 10 Extra Problems for Chapter 10 |
|






|
|
Extra Problems for Chapter 10
1 Find the vector represented by the directed line segment 2 Find the vector A/|B| where A = 5i - 10j, B = 3i - 4j. 3 If A = 7i + 2j, B = -4i + j, find a vector C such that A + B + C = 0. 4 An object originally has position vector P = 12i - 5j and is displaced twice, once by the vector A = 3i + 3j and once by the vector B = 6j. Find the new position vector. 5 Two traders initially have commodity vectors A0 = 18i + 2j, B0 = 20j. They exchange in such a way that their new commodity vectors are equal, A1 = B1. Find their new commodity vectors. 6 Find a vector equation for the line through P(2, 4) with direction vector D = i. 7 Find a vector equation for the line 3x + 4y = - 1. 8 Find the midpoint of the line AB where A = (0, 0), B = (- 4, 2). 9 Find the point of intersection of the diagonals of the parallelogram A(-1,-3),B(0, -3), C(5, 8), D(4, 8). 10 Find the vector represented by 11 Find the direction cosines of A = i - 10j + 2k. 12 If an object at rest has three forces acting on it and two of the forces are F1 = i + 3j - k, F2 = 4i - 3j + 2k, find the third force F3. 13 Find the force required to cause an object of mass 100 to accelerate with the acceleration vector A = i - 5j + 3k. 14 If a trader has the commodity vector A = 5i + 10j + 15k and sells the commodity vector B = 5i + 5j + 5k, find his new commodity vector. 15 Find the vector equation of the line through P(1, 4, 3) and Q(1, 4, 4). 16 Find the vector equation of the line through P(1, 1, 1) with direction cosines (1/2, - 1/2, 1/√2). 17 Determine whether the vectors A = 3i - 4j + 5k, B = 10i + 5j - 2k, are perpendicular. 18 Find the cost of the commodity vector A = 8i + 20j + 10k at the price vector P = 6i + 12j + 15k. 19 Find the amount of work done by a force vector F = 10i - 20j + 5k acting along the displacement vector S = 2i + 3j + 4k. 20 Find a vector in the plane perpendicular to A = - 2i + 3j. 21 Find a vector in space perpendicular to both A = i + j + 2k, B = 2i + j + k. 22 Find two vectors in space perpendicular to each other and to A = i + j + k. 23 Sketch the plane x + 2y + 3z = 6. 24 Sketch the plane 3x - z = 0. 25 Find a scalar equation for the plane through the point (1, 3, 2) with normal vector N = -i - j + 2k. 26 Find a scalar equation for the plane through the points A(4, 1,1), S(2, 3, 4), C(5. 1, 6). 27 Find the point where the line X = 2i - 2j + 4k + ti intersects the plane x + y + z = 1. 28 A bug is crawling along a spoke of a wheel towards the rim at a inches per second. At the same time the wheel is rotating counterclockwise at b radians per second. The center of the wheel is at (0, 0) and at time t = 0, the bug is at (0,0). Find the vector equation for the motion of the bug, 0 ≤ t ≤ 1/a. 29 The sphere x2 + y2 + z2 = 1 is rotating about the z-axis counterclockwise at one radian per second. A bug crawls south al one inch per second along a great circle. At time t = 0 the bug is at (0, 0, 1) and the great circle is in the (x, z) plane. Find the vector equation for the motion of the bug, 0 ≤ t ≤ π. (There are two possible answers.) 30 Find the velocity, speed, and acceleration of the bug in Problem 28. 31 Find the velocity, speed, and acceleration of the bug in Problem 29. 32 Find the derivative of X = (cosh t)i + (sinh t)j. 33 Find the line tangent to the curve
34 Find the length of the curve X = (cosh2 t)i + (sinh2 t)j + (√8sinh r)k, 0 ≤ t ≤ 1. 35 Find the position vector of a particle which moves with velocity V = (et sin et)i + (et cos et)j + etk, if the particle is at the origin at t = 0. 36 If g > 0 is infinitesimal, determine whether or not the vector (sin ε)i + (1 - cos ε)j is infinitesimal. 37 Determine whether or not the vector in Problem 36 has real direction. 38 If ε > 0 is infinitesimal, find the standard part of the vector
39 Let D be a direction vector of a line L in the (x, y) plane. Prove that the set of all direction vectors of L is equal to the set of all scalar multiples of D. 40 Let U and V be perpendicular unit vectors in the plane. Prove that for any vector A, |A|2 = (A · U)2 + (A · V)2. 41 Let U and V be perpendicular unit vectors in the plane. Prove that for any vector A, A = (A · U)U+(A · V)V. Hint: Let B = (A · U)U+ (A · V)V and show that B · U = A · U and B · V = A · V A · U and A · V are called the U and V components of A. 42 Let A and B be two vectors in the plane which are not parallel. Prove that every vector C in the plane can be expressed uniquely in the form C = sA + tB. 43 Prove the Schwartz inequality |A · B| ≤ |A| |B| for vectors A, B in space. 44 Prove that if s and t are positive scalars, then the angle between two vectors A and B in space is equal to the angle between sA and tB. 45 Let p be a plane in space with position vector P and nonparallel direction vectors C and D. Prove that Q is a position vector of p if and only if Q = P + sC + tD for some scalars s and t. Hint: If E is a direction vector of p, then E × D is zero or parallel to C × D, so E × D = s(C × D) for some s, (E - sC) × D = 0, and hence E - sC is parallel to D. 46 Let A, B, C be three distinct points in space whose plane does not pass through the origin. Prove that any vector P may be expressed uniquely in the form P = sA + tB + uC. Hint: Consider the point where the line X = sA intersects the plane with position vector P and direction vectors B and C. 47 Let C be a curve represented by the vector equation X = F(s), 0 ≤ s ≤ b. Assume that the length of the curve from F(0) to F(s) equals s, and that no tangent line crosses the curve. A string is stretched along the curve, attached at the end b, and carefully un-
wrapped starting at 0 as shown in the figure. Show that the point at the end of the string has the position vector P(s) = F(s) + sF'(s). 48 A ball is thrown with initial velocity vector V0 = b(cos αi + sin αj) and position vector S0 = 0 at time t = 0. Its acceleration at time t is A = -32j. Find its position at time t, its maximum height, and the point where it hits the ground.
|
|
Home  Vectors Vectors  Extra Problems for Chapter 10 Extra Problems for Chapter 10 |
|
Last Update: 2006-11-25


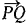 where P = (4, 7), Q = (9, -5).
where P = (4, 7), Q = (9, -5). where P = (4, 2, 1), Q = (9, 6, 0).
where P = (4, 2, 1), Q = (9, 6, 0). at t = 0.
at t = 0.
