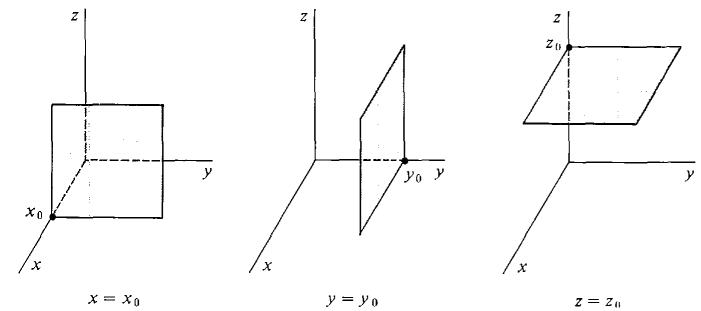| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Surfaces Surfaces  Rectangular Coordinates and the Simplest Planes Rectangular Coordinates and the Simplest Planes |
|






|
|
Rectangular Coordinates and the Simplest Planes
Figure 11.1.1 The rectangular coordinate axes in (x,y,z) space are drawn as in Figure 11.1.1. Points in real space are identified with triples (x, y, z) of real numbers, and points in hyperreal space with triples (x, y, z) of hyperreal numbers. The set of all points for which an equation is true is called the graph, or locus, of the equation. The graph of an equation in the three variables x, y, and z is a surface in space. We have seen in the last chapter that the graph of a linear equation ax + by + cz = d is a plane. The graphs of other equations are often curved surfaces. The simplest planes are: The vertical planes x = x0 perpendicular to the x-axis. The plane x = 0 is called the (y, z) plane. The vertical planes y = y0 perpendicular to the y-axis. The plane y = 0 is called the (x, z) plane. The horizontal planes z = z0 perpendicular to the z-axis. The plane z = 0 is called the (x, y) plane. Examples of the planes x = x0, y = y0 and z = z0 are pictured in Figure 11.1.2.
Figure 11.1.2
|
|
Home  Partial Differentiation Partial Differentiation  Surfaces Surfaces  Rectangular Coordinates and the Simplest Planes Rectangular Coordinates and the Simplest Planes |
|
Last Update: 2006-11-17