| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Total Differentials and Tangent Planes Total Differentials and Tangent Planes  Increment Theorem for Two Variables Increment Theorem for Two Variables |
|||||






|
|||||
Increment Theorem for Two Variables
We shall now state the Increment Theorem. It shows that Δz is very close to dz. INCREMENT THEOREM FOR TWO VARIABLES Suppose z = f(x, y) is smooth at (a, b). Let Δx and Δy be infinitesimal. Then Δz = dz + ε1 Δx + ε2 Δy for some infinitesimals ε1 and ε2 which depend on Δx and Δy. Before proving the Increment Theorem, let us check it for Examples 1 and 2.
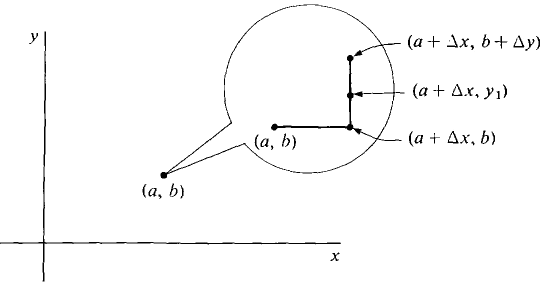
PROOF OF THE INCREMENT THEOREM We break Δz into two parts by going first from (a, b) to (a + Δx, b) and then from (a + Δx, b) to (a + Δx, b + Δy), as shown in Figure 11.4.3,
Figure 11.4.3 Δz = [f(a + Δx,b + Δy) - f(a + Δx, b)] + [f(a + Δx, b) - f(a, b)]. Our plan is as follows. First, we regard f(a, b) as a one-variable function of a and show that (1) f(a + Δx, b) - f(a, b) = fx(a, b) Δx + ε1 Δx for some infinitesimal ε1. Second, we regard f(a + Δx, b) as a one-variable function of b and show that (2) f(a + Δx,b + Δy) - f(a + Δx, b) = fy(a, b) Δy + ε2 Δy for some infinitesimal ε2. Once Equations 1 and 2 are established the proof will be complete because by adding Equations 1 and 2 we get the desired result Δz = fx(a, b) Δx + fy(a, b) Δy + ε1 Δx + ε2 Δy = dz + ε1 Δx + ε2 Δy. Equation 1 follows at once from the one-variable Increment Theorem since fx(a, b) exists. We now prove Equation 2. We regard f(a + Δx, y) as a one-variable function of y. For all y between b and b + Δy, the point (a + Δx, y) is infinitely close to (a, b), so fy(a + Δx, y) is defined. By the one-variable Mean Value Theorem on the interval [b, b + Δy], there is a y1 between b and b + Δy such that
Since fy is continuous at (a, b), fy(a + Δx, y1) =fy (a, b) + ε2, where ε2 is infinitesimal. Then
and Equation 2 follows.
|
|||||
Home  Partial Differentiation Partial Differentiation  Total Differentials and Tangent Planes Total Differentials and Tangent Planes  Increment Theorem for Two Variables Increment Theorem for Two Variables |
|||||
Last Update: 2010-11-25



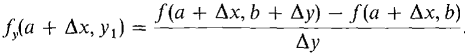
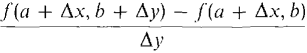 = fy(a, b) + ε2,
= fy(a, b) + ε2,